Bài 61 trang 62 SGK Toán 8 tập 1

Đề bài

Tìm điều kiện của \(x\) để giá trị của biểu thức \(\left( {\dfrac{{5x + 2}}{{{x^2} - 10x}} + \dfrac{{5x - 2}}{{{x^2} + 10x}}} \right).\dfrac{{{x^2} - 100}}{{{x^2} + 4}}\) được xác định.

Tính giá trị của biểu thức tại \(x = 20 040\).

Lời giải chi tiết

+) \({x^2} - 10x = x\left( {x - 10} \right) \ne 0\) khi \(x \ne 0; x - 10 \ne 0\)

Hay \(x \ne 0;\;  x \ne 10\).

+) \({x^2} + 10x = x\left( {x + 10} \right) \ne 0\) khi \(x \ne 0; x + 10 \ne 0\)

Hay \(x \ne 0;\;  x \ne  - 10\).

+) \({x^2} + 4 >0\) do \({x^2} \geqslant 0\) với mọi giá trị của \(x\).

Vậy điều kiện của biến \(x\) để biểu thức đã cho được xác định là  \(x \ne  - 10,\; x \ne 0,\; x \ne 10\).

Để việc tính giá trị của biểu thức được đơn giản hơn ta rút gọn biểu thức trước:

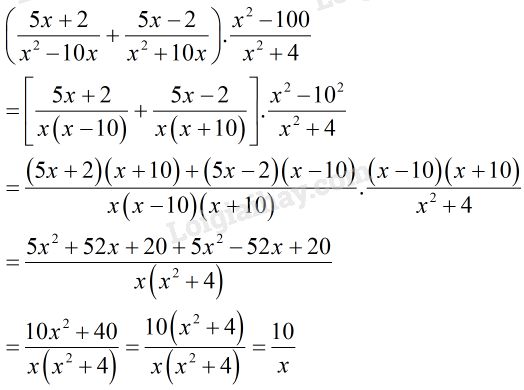
\(x = 20040\) thỏa mãn điều kiện của biến.

Vậy với \(x = 20040\) biểu thức có giá trị là \(\dfrac{{10}}{{20040}} = \dfrac{1}{{2004}}\).