Câu 4 trang 210 sách bài tập Giải tích 12 Nâng cao

Cho hàm số

\(f\left( x \right) = {1 \over 3}{x^3} + {x^2} - {5 \over 3}\)

LG a

Khảo sát sự biến thiên và vẽ đồ thị  (G) của hàm số f

Lời giải chi tiết:

\(y' = {x^2} + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\)

Bảng biến thiên :

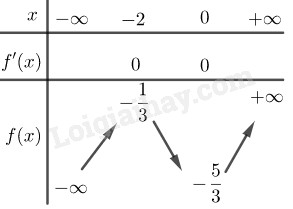
Đồ thị:

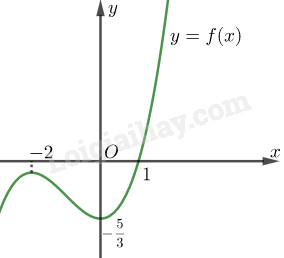
LG b

Viết phương trình tiếp tuyến (G) đi qua điểm \(M\left( { - {7 \over 3};{1 \over 3}} \right)\)

Lời giải chi tiết:

Có hai tiếp tuyến cùng đi qua M là đường thẳng \(y = 3x + {{22} \over 3}\) và đường thẳng\(y =  - x - 2\).

LG c

Chứng minh rằng (G) nhận điểm \(U\left( { - 1; - 1} \right)\) làm tâm đối xứng.

Lời giải chi tiết:

\(y'' = 2x + 2 = 0 \Leftrightarrow x =  - 1 \Rightarrow y =  - 1\)

Suy ra (G) nhận điểm \(U\left( { - 1; - 1} \right)\) làm tâm đối xứng.