Câu 2 trang 209 sách bài tập Giải tích 12 Nâng cao

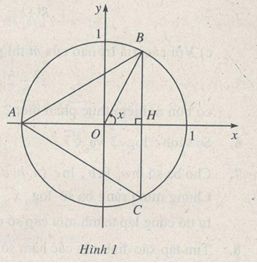
Trong mặt phẳng tọa độ \(\left( {O,\overrightarrow i ,\overrightarrow j } \right)\) cho tam giác ABC đỉnh A(-1;0), AB = AC, nội tiếp trong đường tròn đơn vị, đỉnh B nằm phía trên trục hoành. Gọi x là số đo bằng rađian của góc \(\left( {\overrightarrow i ,\overrightarrow {OB} } \right),0 < x < \pi \) (h.1).

LG a

Tính diện tích S của tam giác ABC theo x.

Lời giải chi tiết:

\(S = \sin (1 + \cos x)\)

LG b

Với giá trị nào của x, tam giác ABC có diện tích lớn nhất.         

Lời giải chi tiết:

\(x = {\pi  \over 3}\); \(\max S = {{3\sqrt 3 } \over 4}\) .