Bài 98 trang 122 SBT toán 9 tập 1

Đề bài

Cho tam giác \(AB = 6cm,\) \(AC = 4,5cm,\)\( BC = 7,5cm.\)

a) Chứng minh tam giác \(ABC\) vuông tại \(A\). Tính các góc \(\widehat B,\widehat C\) và đường cao \(AH\) của tam giác.

b) Tìm tập hợp các điểm \(M\) sao cho \({S_{ABC}} = {S_{BMC}}.\)

Lời giải chi tiết

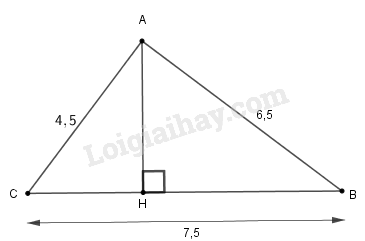
a) Ta có:

\(A{B^2} = {6^2} = 36\)

\(A{C^2} = 4,{5^2} = 20,25\)

\(B{C^2} = 7,{5^2} = 56,25\)

Vì \(A{B^2} + A{C^2} = 36 + 20,25\)\( = 56,25 = B{C^2}\) nên tam giác \(ABC\) vuông tại \(A\) ( theo định lí Pi-ta-go đảo).

Kẻ \(AH \bot BC\)

Ta có: \(AH = \displaystyle {{AB.AC} \over {BC}} = {{6.4,5} \over {7,5}} = 3,6\,(cm)\)

\(\sin \widehat C = \displaystyle {{AC} \over {BC}} = {{4,5} \over {7,5}} = 0,6\)

Suy ra: \(\widehat C = 53^\circ 8'\)

Ta có:

\(\widehat B + \widehat C = 90^\circ\)  \(\Rightarrow \widehat B = 90^\circ  - \widehat C\)\( = 90^\circ  - 53^\circ 8' = 36^\circ 52'\)

b) Tam giác \(ABC\) và tam giác \(MBC\) có chung cạnh đáy \(BC\), đồng thời \({S_{ABC}} = {S_{MBC}}\)  nên khoảng cách từ \(M\) đến \(BC\) bằng khoảng cách từ \(A\) đến \(BC\). Vậy \(M\) thay đổi cách \(BC\) một khoảng bằng \(AH\) nên \(M\) nằm trên hai đường \(x\) và \(y\) song song với \(BC\) cách \(BC\) một khoảng bằng \(AH\).