Bài 96 trang 112 SBT toán 9 tập 1

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) chia cạnh huyền \(BC\) thành hai đoạn \(BH, CH\) có độ dài lần lượt là \(4cm, 9cm\). Gọi \(D\) và \(E\) lần lượt là hình chiếu của \(H\) trên \(AB\) và \(AC\). 

a) Tính độ dài đoạn thẳng \(DE\).

b) Các đường thẳng vuông góc với \(DE\) tại \(D\) và tại \(E\) lần lượt cắt \(BC\) tại \(M\) và \(N\). Chứng minh \(M\) là trung điểm của \(BH\) và \(N\) là trung điểm của \(CH\).

c) Tính diện tích tứ giác \(DENM\).

Lời giải chi tiết

a) Ta có: 

\(HD \bot AB \Rightarrow \widehat {ADH} = 90^\circ \)

\(HE \bot AC \Rightarrow \widehat {AEH} = 90^\circ \)

Tứ giác \(ADHE\) có \(3\) góc vuông nên nó là hình chữ nhật.

Suy ra: \(AH = DE\) (tính chất hình chữ nhật)

Tam giác \(ABC\) vuông tại \(A\) và có \(AH\) là đường cao.

Theo hệ thức liên hệ giữa đường cao và hình chiếu ta có:

\(\eqalign{
& A{H^2} = HB.HC = 4.9 = 36 \cr 
& \Rightarrow AH = 6\,(cm) \cr} \)

Vậy \(DE = 6 (cm)\)

b) * Gọi \(G\) là giao điểm của \(AH\) và \(DE\)

Ta có: \(GA = GD = GH = GE\) (tính chất hình chữ nhật)

Suy ra tam giác \(GHD\) cân tại \(G\)

Ta có:

\(\widehat {GDH} = \widehat {GHD}\,(1)\)

\(\widehat {GDH} + \widehat {MDH} = 90^\circ \,(2)\)

\(\widehat {GHD} + \widehat {MHD} = 90^\circ \,(3)\)

Từ (1), (2) và (3) suy ra: \(\widehat {MDH} = \widehat {MHD}\,(4)\)

Suy ra tam giác \(MDH\) cân tại \(M\) \( \Rightarrow MD = MH\,(5)\)

Lại có: \(\widehat {MDH} + \widehat {MDB} = 90^\circ \,(6)\)

\(\widehat {MBD} + \widehat {MHD} = 90^\circ \) (\(∆BDH\) vuông tại \(D\)) (7)

Từ (4), (6) và (7) suy ra: \(\widehat {MDB} = \widehat {MBD}\)

Suy ra tam giác \(MBD\) cân tại \(M\) \( \Rightarrow MB = MD\,(8)\)

 Từ (5) và (8) suy ra: \(MB = MH\) hay \(M\) là trung điểm của \(BH\).

*Tam giác \(GHE\) cân tại \(G\)

Ta có: \(\widehat {GHE} = \widehat {GEH}\,(9)\)

\(\widehat {GHE} + \widehat {NHE} = 90^\circ \) (10)

\(\widehat {GEH} + \widehat {NEH} = 90^\circ \) (11)

Từ (9), (10) và (11) suy ra: \(\widehat {NHE} = \widehat {NEH}\) (12)

Suy ra tam giác \(NEH\) cân tại \(N\) \( \Rightarrow NE = NH\) (13)

Lại có: \(\widehat {NEC} + \widehat {NEH} = 90^\circ \) (14)

\(\widehat {NHE} + \widehat {NCE} = 90^\circ \) (\(∆CEH\) vuông tại \(E\)) (15)

Từ (12), (14) và (15) suy ra: \(\widehat {NDC} = \widehat {NCE}\)

Suy ra tam giác \(NCE\) cân tại \(N\) \( \Rightarrow NC = NE\,(16)\)

Từ (13) và (16) suy ra: \(NC = NH\) hay \(N\) là trung điểm của \(CH\). 

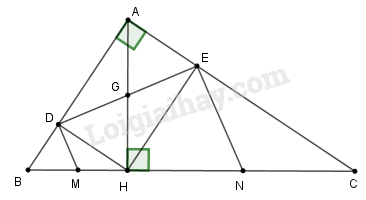
c) Tam giác \(BDH\) vuông tại \(D\) có \(DM\) là đường trung tuyến nên:

\(DM = \displaystyle {1 \over 2}BH = {1 \over 2}.4 = 2\,(cm)\)

Tam giác CEH vuông tại E có EN là đường trung tuyến nên

\(EN = \displaystyle {1 \over 2}CH = {1 \over 2}.9 = 4,5\,(cm)\)

Mà \(MD \bot DE\) và \(NE \bot DE\) nên \(MD // NE\)

Suy ra tứ giác \(DENM\) là hình thang

Vậy 

\(\eqalign{
& {S_{DENM}} = {{DM + NE} \over 2}.DE \cr 
& = {{2 + 4,5} \over 2}.6 = 19,5cm^2. \cr} \)