Bài 95 trang 122 SBT toán 9 tập 1

Đề bài

Cho tam giác \(ABC\) có góc \(B\) bằng \(120^\circ, \) \(BC = 12cm, AB = 6cm\). Đường phân giác của góc \(B\) cắt cạnh \(AC\) tại \(D\).

a) Tính độ dài đường phân giác \(BD\).

b) Gọi \(M\) là trung điểm của \(BC\). Chứng minh \(AM \bot BD.\)

Lời giải chi tiết

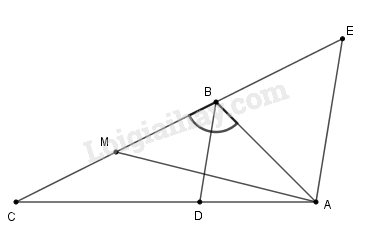
a) Ta có: 

\(\widehat {ABD} = \widehat {CBD} = \displaystyle {{\widehat {ABC}} \over 2}\)\( = \displaystyle {{120^\circ } \over 2}\)\( = 60^\circ \)

Từ \(A\) kẻ đường thẳng song song với \(BD\) cắt \(CB\) tại \(E\).

Lại có:

\(\widehat {BAE} = \widehat {ABD} = 60^\circ \) (so le trong)

 \(\widehat {CBD} = \widehat {AEB} = 60^\circ \) (đồng vị)

Suy ra tam giác \(ABE\)  đều 

\( \Rightarrow AB = BE = EA = 6\,(cm)\,\,(1)\)

Khi đó: \(CE = BC + BE = 12 + 6 = 18 (cm)\)

Tam giác \(ACE\) có \(AE // BD\) nên suy ra:

\(\displaystyle {{BC} \over {CE}} = {{BD} \over {AE}} \) 
\(\Rightarrow BD = \displaystyle {{BC.AE} \over {CE}} = {{12.6} \over {18}} = 4\,(cm) \)

b) Ta có: 

\(MB = MC = \displaystyle {1 \over 2}.BC = {1 \over 2}.12\)\( = 6\,(cm)\,\,(2)\)

Từ (1) và (2) suy ra:

\(BM = AB \Rightarrow \) \(∆ABM\) cân tại \(B\).

Tam giác cân \(ABM\) có \(BD\) là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy \(BD \bot AM\)