Giải mục 1 trang 16, 17 SGK Toán 11 tập 1 - Cánh Diều

Hoạt động 1

Cho tam giác MNP có đường cao PQ (Hình 17).

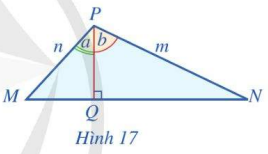
a)     Viết công thức tính PQ theo cạnh n và góc a; công thức tính PQ theo cạnh m và góc b

b)     Viết công thức tính diện tích mỗi tam giác MPQ, NPQ, MNP theo các cạnh m, n và các cạnh m, n và các góc a, b, a + b

c)     Sử dụng kết quả: \({S_{MPN}} = {S_{MPQ}} + {S_{NPQ}}\), hãy tìm công thức tính \(\sin \left( {a + b} \right)\) theo \(\sin a,\cos a,\sin b,\cos b\). Từ đó rút ra đẳng \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b\,\,\,\left( * \right)\)

d)     Tính \(\sin \left( {a - b} \right)\) bằng cách biến đổi \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right]\) và sử dụng công thức (*)

Phương pháp giải:

Dựa vào công thức sin, cos đã học để xác định

Lời giải chi tiết:

a)     \(PQ = n.\cos a,PQ = m.\cos b\)

b)     \(MQ = n.\sin a,PN = m.\sin b \Rightarrow MN = n.\sin a + m.\sin b\)

\(\begin{array}{l}{S_{MPQ}} = \frac{1}{2}m.\cos b.n.\sin a = \frac{1}{2}m.n.\cos b.\sin a\\{S_{NPQ}} = \frac{1}{2}n.\cos a.m.\sin b = \frac{1}{2}m.n.\cos a.\sin b\\{S_{MNP}} = \frac{1}{2}m.n.\sin \left( {a + b} \right)\end{array}\)

c)     \({S_{MNP}} = {S_{MPQ}} + {S_{NPQ}} \Rightarrow \frac{1}{2}m.n.\cos b.\sin a + \frac{1}{2}m.n.\cos a.\sin b = \frac{1}{2}m.n.\sin \left( {a + b} \right)\)

\( \Rightarrow \sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\)

d)     \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right] = \sin a.\cos \left( { - b} \right) + \cos a.\sin \left( { - b} \right) = \sin a.\cos b - \cos a.\sin b\)

Luyện tập - Vận dụng

Tính \(\sin \frac{\pi }{{12}}\)

Phương pháp giải:

Sử dụng công thức cộng đối với sin

Lời giải chi tiết:

Áp dụng công thức cộng, ta có:

\(\begin{array}{l}\sin \frac{\pi }{{12}} = \sin \left( {\frac{\pi }{4} - \frac{\pi }{6}} \right) = \sin \frac{\pi }{4}.\cos \frac{\pi }{6} - \cos \frac{\pi }{4}.\sin \frac{\pi }{6}\\ = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} - \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6  - \sqrt 2 }}{4}\end{array}\)

Hoạt động 2

a)     Tính \(\cos \left( {a + b} \right)\) bằng cách biến đổi \(\cos \left( {a + b} \right) = \sin \left[ {\frac{\pi }{2} - \left( {a + b} \right)} \right] = \sin \left[ {\left( {\frac{\pi }{2} - a} \right) - b} \right]\) và sử dụng công thức cộng đối với sin

b)     Tính \(\cos \left( {a - b} \right)\) bằng cách biến đổi \(\cos \left( {a - b} \right) = \cos \left[ {a + \left( { - b} \right)} \right]\) và sử dụng công thức \(\cos \left( {a + b} \right)\) có được ở câu a

Phương pháp giải:

Dựa vào công thức cộng sin đã chứng minh ở bên trên để tính

Lời giải chi tiết:

a)     \(\cos \left( {a + b} \right) = \sin \left[ {\left( {\frac{\pi }{2} - a} \right) - b} \right] = \sin \left( {\frac{\pi }{2} - a} \right).\cos b - \cos \left( {\frac{\pi }{2} - a} \right).\sin b = \cos a.\cos b - \sin a.\sin b\)

b)     \(\cos \left( {a - b} \right) = \cos \left[ {a + \left( { - b} \right)} \right] = \cos a.\cos \left( { - b} \right) - \sin a.\sin \left( { - b} \right) = \sin a.\sin b + \cos a.\cos b\)

Luyện tập - Vận dụng 2

Tính \(\cos {15^ \circ }\)

Phương pháp giải:

Sử dụng công thức cộng dối với cosin

Lời giải chi tiết:

Áp dụng công thức cộng, ta có:

\(\begin{array}{l}\cos {15^ \circ } = \cos ({45^ \circ } - {30^ \circ }) = \cos {45^ \circ }\cos {30^ \circ } + \sin {45^ \circ }\sin {30^ \circ }\\ = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6  + \sqrt 2 }}{4}\end{array}\)

Hoạt động 3

a)     Sử dụng công thức cộng đối với sin và côsin, hãy tính \(\tan \left( {a + b} \right)\) theo tan a và tan b khi các biểu thức đều có nghĩa

b)     Khi các biểu thức đều có nghĩa, hãy tính \(\tan \left( {a - b} \right)\) bằng cách biến đổi \(\tan \left( {a - b} \right) = \tan \left[ {a + \left( { - b} \right)} \right]\) và sử dụng công thức \(\tan \left( {a + b} \right)\) có được ở câu a.

Phương pháp giải:

Dựa vào công thức cộng sin, cos đã chứng minh ở bên trên để tính

Lời giải chi tiết:

a)     \(\tan \left( {a + b} \right) = \frac{{\sin \left( {a + b} \right)}}{{\cos \left( {a + b} \right)}} = \frac{{\sin a.\cos b + \cos a.\sin b}}{{\cos a.\cos b - \sin a.\sin b}}\)

\(\begin{array}{l} = \frac{{\sin a.\cos b + \cos a.\cos b}}{{\cos a.\cos b - \sin a.\sin b}} = \frac{{\sin a.\cos b}}{{\cos a.\cos b - \sin a.\sin b}} + \frac{{\cos a.\sin b}}{{\cos a.\cos b - \sin a.\sin b}}\\ = \frac{{\frac{{\sin a.\cos b}}{{\cos a.\cos b}}}}{{\frac{{\cos a.\cos b - \sin a.\sin b}}{{\cos a.\cos b}}}} + \frac{{\frac{{\cos a.\sin b}}{{\cos a.\cos b}}}}{{\frac{{\cos a.\cos b - \sin a.\sin b}}{{\cos a.\cos b}}}} = \frac{{\tan a}}{{1 - \tan a.\tan b}} + \frac{{\tan b}}{{1 - \tan a.\tan b}}\\ = \frac{{\tan a + \tan b}}{{1 - \tan a.\tan b}}\end{array}\)

\( \Rightarrow \tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a.\tan b}}\)

b)      

\(\tan \left( {a - b} \right) = \tan \left( {a + \left( { - b} \right)} \right) = \frac{{\tan a + \tan \left( { - b} \right)}}{{1 - \tan a.\tan \left( { - b} \right)}} = \frac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}\)

Luyện tập - Vận dụng

Tính \(\tan {165^ \circ }\)

Phương pháp giải:

Sử dụng công thức cộng đối với tang

Lời giải chi tiết:

\(\begin{array}{l}\tan {165^ \circ } = \tan ({105^ \circ } + {60^ \circ }) = \frac{{\tan {{105}^ \circ } + \tan {{60}^ \circ }}}{{1 - \tan {{105}^ \circ }.\tan {{60}^ \circ }}}\\ = \frac{{ - 2 - \sqrt 3  + \sqrt 3 }}{{1 - ( - 2 - \sqrt 3 ).\sqrt 3 }} =  - 2 + \sqrt 3 \end{array}\)