Bài 7 trang 202 SBT Hình học 10
Giải bài 7 trang 202 sách bài tập Hình học 10. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : {x^2} + {y^2} - 6x - 6y + 14 = 0 . Tìm điểm M thuộc trục hoành sao cho từ M kẻ được hai tiếp tuyến của (C) mà góc giữa hai tiếp tuyến đó bằng 60.
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({x^2} + {y^2} - 6x - 6y + 14 = 0\) . Tìm điểm M thuộc trục hoành sao cho từ M kẻ được hai tiếp tuyến của (C) mà góc giữa hai tiếp tuyến đó bằng \({60^ \circ }\) .
Lời giải chi tiết
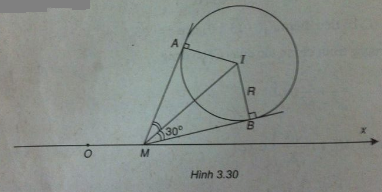
Đường tròn (C) có tâm I(3 ; 3) và có bán kính
\(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {9 + 9 - 14} = 2\)
Điểm \(M(x;0)\) thuộc Ox.
Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:
\(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\)
\( \Rightarrow IM = \frac{R}{{\sin {{30}^ \circ }}} = 2R = 4\).
\(IM = 4 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2} + 9} = 4\)
\( \Leftrightarrow {x^2} - 6x + 2 = 0\)
\( \Leftrightarrow x = 3 \pm \sqrt 7 \) .
Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là :
\({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 - \sqrt 7 ;0} \right)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7 trang 202 SBT Hình học 10 timdapan.com"







