Bài 10 trang 202 SBT Hình học 10

Đề bài

Trong mặt phẳng tọa độ Oxy, cho elip (E) : \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) . Gọi hai tiêu điểm của (E) lần lượt là  \({F_1},{F_2}\) và M thuộc (E) sao cho \(\widehat {{F_1}M{F_2}} = {60^ \circ }\) . Tìm tọa độ điểm M và tính diện tích tam giác \(M{F_1}{F_2}\) .

Lời giải chi tiết

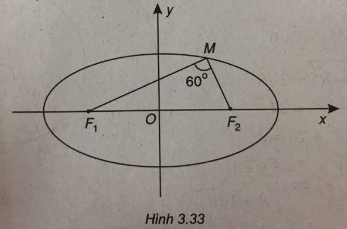
Elip (E) có phương trình chính tắc : \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1.\)

Ta có : \(a = 5,b = 3\) . Suy ra \({c^2} = {a^2} - {b^2} = 25 - 9 = 16.\)

Vậy \(c = 4.\)

Xét điểm \(M\left( {x;y} \right)\) thuộc elip, ta có \(\left\{ \begin{array}{l}{F_1}M = a + \frac{c}{a}x = 5 + \frac{4}{5}x\\{F_2}M = a - \frac{c}{a}x = 5 - \frac{4}{5}x\end{array} \right.\)

Áp dụng định lí côsin trong tam giác \({F_1}M{F_2}\) ta có :

\({F_1}F_2^2 = MF_1^2 + MF_2^2 - 2M{F_1}.M{F_2}\cos {60^ \circ }\)

\( \Leftrightarrow 4{c^2} = {\left( {5 + \frac{4}{5}x} \right)^2} + {\left( {5 - \frac{4}{5}x} \right)^2} - 2\left( {25 - \frac{{16}}{{25}}{x^2}} \right).\frac{1}{2}\)

\( \Leftrightarrow 64 = 25 + \frac{{48}}{{25}}{x^2} \Leftrightarrow {x^2} = \frac{{25}}{{16}}.13 \Leftrightarrow x =  \pm \frac{5}{4}\sqrt {13} \,\,\,\,\,\,\,\,(1)\)

Ta lại có \(M \in \left( E \right) \Rightarrow \frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\,\,\,(2)\)

Thay (1) vào phương trình (2) ta được

\(\frac{{{y^2}}}{9} = 1 - \frac{{13}}{{16}} \Leftrightarrow {y^2} = \frac{9}{{16}}.3 \Leftrightarrow y =  \pm \frac{3}{4}\sqrt 3 .\)

Vậy có bốn điểm M thỏa mãn đề bài. Chúng có tọa độ là \(\left( { \pm \frac{5}{4}\sqrt {13} ; \pm \frac{3}{4}\sqrt 3 } \right).\)