Bài 18 trang 203 SBT Hình học 10

Đề bài

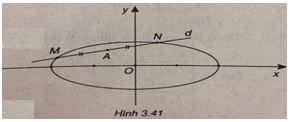
Trong mặt phẳng tọa độ Oxy, cho elip (E) : \(\frac{{{x^2}}}{4} + {y^2} = 1\) và điểm \(A\left( { - 1;\frac{1}{2}} \right)\) . Gọi d là đưởng thẳng đi qua A có hệ số góc là m. Xác định m để d cắt (E) tại hai điểm phân biệt M và N sao cho A là trung điểm của MN.

Lời giải chi tiết

Phương trình đường thẳng d có dạng

\(y - \frac{1}{2} = m(x + 1)\)

\( \Leftrightarrow y = m(x + 1) + \frac{1}{2}.\)

Phương trình hoành độ giao điểm của d và (E) là :

\(\frac{{{x^2}}}{4} + {\left( {mx + m + \frac{1}{2}} \right)^2} = 1\) \( \Leftrightarrow {x^2} + 4{\left[ {mx + \left( {m + \frac{1}{2}} \right)} \right]^2} = 4\)

\( \Leftrightarrow \left( {4{m^2} + 1} \right){x^2} + 4\left[ {\left( {2m + 1} \right)m} \right]x \) \(+ 4{\left( {m + \frac{1}{2}} \right)^2} - 4 = 0.\)

A là trung điểm của MN \( \Leftrightarrow \frac{{{x_M} + {x_N}}}{2} = {x_A} \Leftrightarrow \frac{{ - 4(2{m^2} + m)}}{{2(4{m^2} + 1)}} =  - 1\)

\( \Leftrightarrow 4{m^2} + 2m = 4{m^2} + 1 \Leftrightarrow m = \frac{1}{2}.\)