Bài 11 trang 202 SBT Hình học 10

Đề bài

Trong mặt phẳng tọa độ Oxy, cho ba điểm I(2 ; 4), B(1 ; 1), C(5 ; 5). Tìm điểm A sao cho I là tâm đường tròn nội tiếp tam giác ABC.

Lời giải chi tiết

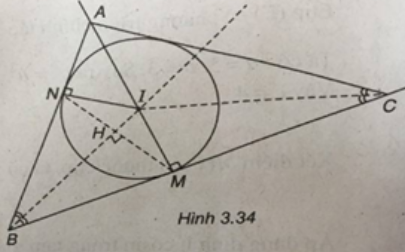
Ta có : \(IB = \sqrt {{{\left( {1 - 2} \right)}^2} + {{\left( {1 - 4} \right)}^2}}  = \sqrt {10} \)

\(\begin{array}{l}IC = \sqrt {{{(5 - 2)}^2} + {{(5 - 4)}^2}}  = \sqrt {10} \\IB = IC \Rightarrow AB = AC.\end{array}\)

Gọi M là trung điểm của BC, ta có M(3 ; 3).

Phương trình đường thẳng \(IM:x + y - 6 = 0\,\,\,\,\,\,\,\,\,\,(1)\)

Phương trình đường thẳng \(IB:3x - y - 2 = 0\,\,\,\,\,\,\,\,\,(2)\)

Gọi N là điểm đối xứng với M qua đường thẳng IB.

Đặt N(x;y), ta có tọa độ trung điểm H của MN là \(\left( {\frac{{x + 3}}{2};\frac{{y + 3}}{2}} \right).\)

\(\overrightarrow {MN}  = (x - 3;y - 3)\)

\(\overrightarrow {BI}  = (1;3)\)

Ta có : \(\left\{ \begin{array}{l}\overrightarrow {MN} .\overrightarrow {BI}  = 0\\H \in IB\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x - 3 + 3(y - 3) = 0\\3\left( {\frac{{x + 3}}{2}} \right) - \left( {\frac{{y + 3}}{2}} \right) - 2 = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x + 3y - 12 = 0\\3x - y + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{3}{5}\\y = \frac{{19}}{5}.\end{array} \right.\)

Vậy \(N\left( {\frac{3}{5};\frac{{19}}{5}} \right).\)

Ta có B(1 ; 1). Phương trình đường thẳng \(BN:7x + y - 8 = 0.\)

Điểm A là giao của hai đường thẳng BN và IM nên tọa độ của A là nghiệm của hệ phương trình

\( \Leftrightarrow \left\{ \begin{array}{l}7x + y - 8 = 0\\x + y - 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{3}\\y = \frac{{17}}{3}\end{array} \right.\)

Vậy tọa độ điểm A là \(\left( {\frac{1}{3};\frac{{17}}{3}} \right).\)