Bài 21 trang 204 SBT Hình học 10

Đề bài

Trong mặt phẳng tọa độ Oxy, lập phương trình chính tắc của elip (E) biết (E) có tiêu điểm \({F_1}\left( { - 2;0} \right)\) và diện tích hình chữ nhật cơ sở bằng \(12\sqrt 5 \) .

Viết phương trình đường tròn (C) có tâm là gốc tọa độ và (C) cắt (E) tại bốn điểm tạo thành hình vuông.

Lời giải chi tiết

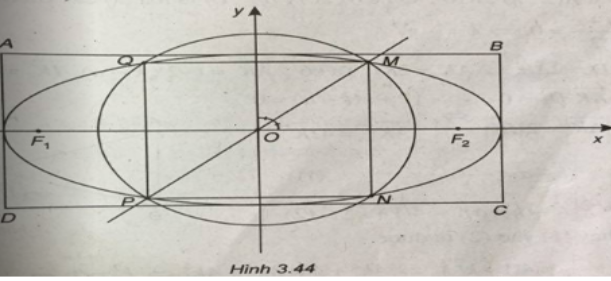
Phương trình elip có dạng \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.\)

Ta có tiêu điểm \({F_1}\left( { - 2;0} \right)\). Suy ra c = 2.

Diện tích hình chữ nhật cơ sở ABCD là 4ab.

Suy ra \(4ab = 12\sqrt 5 \).

Ta có : \({a^2} = {b^2} + {c^2} = {b^2} + 4.\)

Giải hệ phương trình : \(\left\{ \begin{array}{l}ab = 3\sqrt 5 \\{a^2} = {b^2} + 4\end{array} \right.\) ta được \(\left\{ \begin{array}{l}a = 3\\b = \sqrt 5 .\end{array} \right.\)

Vậy phương trình elip là : \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1.\)

Đường tròn (C) tâm O, bán kính R cắt elip tại bốn điểm M, N, P, Q.

Ta có MNPQ là hình vuông suy ra phương trình đường thẳng OM là : \(y = x.\)

Thay \(y = x\) vào phương trình elip ta được

\({R^2} = O{M^2} = x_M^2 + y_M^2 = \frac{{45}}{7}.\)

Vậy phương trình đường tròn  (C)  là : \({x^2} + {y^2} = \frac{{45}}{7}\) .