Bài 5 trang 221 SGK Đại số 10 Nâng cao

LG a

Lập bảng biến thiên và vẽ đồ thị (p) của : y = x² + x - 6

Lời giải chi tiết:

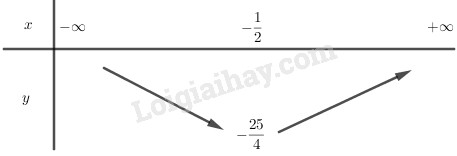
\(\begin{array}{l} - \frac{b}{{2a}} =  - \frac{1}{2}\\ - \frac{\Delta }{{4a}} =  - \frac{{25}}{4}\end{array}\)

Hàm số bậc hai có \(a = 1 > 0\) nên đồng biến trên \(\left( { - \frac{1}{2}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\)

Bảng biến thiên:

Đồ thị:

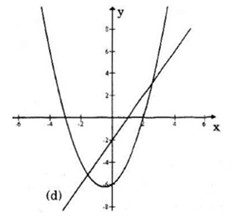
Đồ thị là Parabol có đỉnh I(-1/2;-25/4)

Nhận x=-1/2 làm trục đối xứng

Cắt Oy tại (0;6) và cắt Ox tại các điểm (-3;0) và (2;0).

LG b

Biện luận theo m số giao điểm của (P) và đường thẳng (d): y = 2x + m

Lời giải chi tiết:

Số giao điểm của parabol (P) với đường thẳng (d) đúng bằng số nghiệm của phương trình:

x² + x- 6 = 2x + m hay x² – x – 6 – m = 0   (1)

Phương trình (1) có biệt thức:

Δ = 1 + 4(6 + m) = 4m + 25

Do đó:

+ Nếu \(m <  - {{25} \over 4} \Rightarrow \Delta  < 0\) thì phương trình (1) vô nghiệm

Do đó, (P) và (d) không có điểm chung

+ Nếu \(m =  - {{25} \over 4} \Rightarrow \Delta  =0\) thì phương trình (1) có 1 nghiệm kép duy nhất

Do đó, (P) và (d) có 1 điểm chung

+ Nếu \(m >  - {{25} \over 4} \Rightarrow \Delta  > 0\) thì phương trình (1) có hai nghiệm phân biệt.

LG c

Khi (d) và (P) cắt nhau, gọi A và B là giao điểm, hãy tìm tọa độ trung điểm của đoạn thẳng AB.

Lời giải chi tiết:

Giả sử (P) và (d) cắt nhau tại hai điểm phân biệt. Khi đó hoành độ của A và B chính là hai nghiệm của phương trình (1), gọi chúng là x₁ và x₂.

Hơn nữa, A và B là hai  điểm của đường thẳng (d) nên tọa độ của chúng là:

\(A({x_1};\,2{x_1} + m)\,;\) \(B({x_2};\,2{x_2} + m)\,\,\,(m >  - {{25} \over 4})\)

Vậy trung điểm của đoạn thẳng AB có tọa độ là: \(I({{{x_1} + {x_2}} \over 2};\,{x_1} + {x_2} + m)\)

Theo định lý Vi-ét, ta có: x₁ + x₂ = 1

Tọa độ điểm I là \(({1 \over 2};\,1 + m)\,\,\,\,(m >  - {{25} \over 4})\)