Bài 1.91 trang 29 SBT Giải tích 12 Nâng cao

Cho hàm số \(y = {{2{x^2} + 3x + 3} \over {x + 1}}\)

LG a

Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.

Lời giải chi tiết:

Ta có: \(y = \frac{{2{x^2} + 3x + 3}}{{x + 1}} = 2x + 1 + \frac{2}{{x + 1}}\)

+) TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)

+) Chiều biến thiên:

\(\mathop {\lim }\limits_{x \to  - {1^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to  - {1^ - }} y =  - \infty \) nên TCĐ \(x =  - 1\).

\(\mathop {\lim }\limits_{x \to  \pm \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to  \pm \infty } \left( {\frac{2}{{x + 1}}} \right) = 0\) nên TCX: \(y = 2x + 1\).

Ta có:

\(\begin{array}{l}y' = 2 - \frac{2}{{{{\left( {x + 1} \right)}^2}}}\\y' = 0 \Leftrightarrow 2 - \frac{2}{{{{\left( {x + 1} \right)}^2}}} = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 1\\x + 1 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\end{array}\)

BBT:

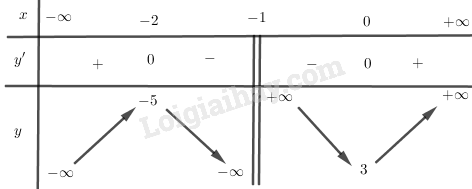
+) Đồ thị:

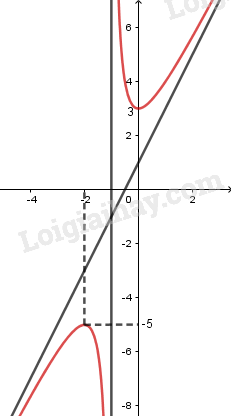
LG b

Dựa vào đồ thị, hãy biện luận số giao điểm của đường thẳng \(y = m(x + 1) + 3\) và đường cong (C), tùy theo các giá trị của m.

Lời giải chi tiết:

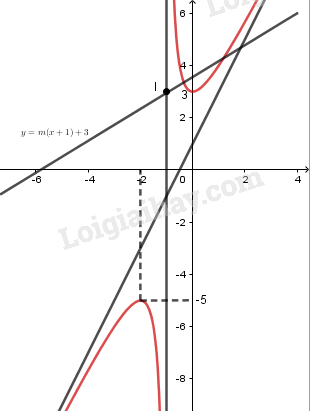
Đường thẳng y = m(x + 1) + 3 có hệ số góc m, đi qua điểm I(-1;3) nằm trên tiệm cận đứng x = -1 của (C).

- Với m < 0 đường thẳng không cắt đường cong (C)

- Với m = 0 đường thẳng tiếp xúc với (C) tại điểm (0;3)

- Với 0 < m < 2 đường thẳng cắt (C) tại hai điểm (cả hai giao điểm đều phải thuộc nhánh phải của (C)

- Với m = 2, đường thẳng song song với tiệm cận xiên của (C); đường thẳng cắt (C) tại một điểm.

- Với m > 2, đường thẳng cắt (C) tại hai điểm thuộc hai nhánh của (C).