Bài 1.85 trang 28 SBT Giải tích 12 Nâng cao

LG a

Khảo sát sự biến thiên và vẽ đồ thị  (C) của hàm số

\(y =  - {x^4} - 2{x^2} + 3\)

Lời giải chi tiết:

+) TXĐ: \(D = \mathbb{R}\)

+) Chiều biến thiên:

\(\mathop {\lim }\limits_{x \to  \pm \infty } y =  - \infty \)

\(\begin{array}{l}y' =  - 4{x^3} - 4x\\y' = 0 \Leftrightarrow  - 4{x^3} - 4x = 0\\ \Leftrightarrow  - 4x\left( {{x^2} + 1} \right) = 0\\ \Leftrightarrow x = 0\end{array}\)

BBT:

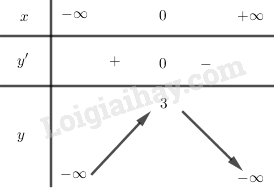
Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\).

Hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).

Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = 3\).

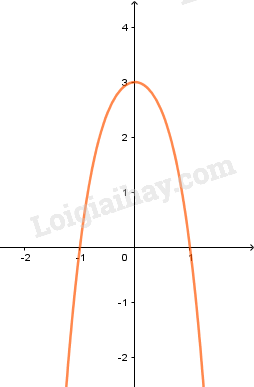
+) Đồ thị:

LG b

Với giá trị nào của m, đường thẳng \(y = 8x + m\) là tiếp tuyến của đường cong (C)?

Lời giải chi tiết:

Ta có \(y' =  - 4{x^3} - 4x\)

Hoành độ có tiếp điểm của đường thẳng và đường cong (C) là nghiệm của phương trình

\( - 4{x^3} - 4x = 8\)

\(\eqalign{&  \Leftrightarrow {x^3} + x + 2 = 0  \cr &  \Leftrightarrow \left( {x + 1} \right)({x^2} - x + 2) = 0\cr& \Leftrightarrow x =  - 1 \cr} \)

M(-1;0) là tiếp điểm của đường thẳng và (C).

Vì điểm M nằm trên đường thẳng nên \(8\left( { - 1} \right) + m = 0 \).

\(\Leftrightarrow m = 8\)