Bài 1.7 trang 11 SBT Giải tích 12 Nâng cao

Đề bài

Với các giá trị nào của m, hàm số

\(y = x + 2 + {m \over {x - 1}}\)

Đồng biến trên mỗi khoảng xác định của nó ?

Lời giải chi tiết

Ta có \(y' = 1 - {m \over {{{(x - 1)}^2}}}\) với mọi \(x \ne 1\)

+) Nếu \(m \le 0\) thì y’ > 0 với mọi \(x \ne 1\) . Do đó hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)

+) Nếu m > 0 thì

\(y' = {{{x^2} - 2x + 1 - m} \over {{{(x - 1)}^2}}}\)

\(y' = 0 \Leftrightarrow {x^2} - 2x + 1 - m = 0\) \( \Leftrightarrow x = 1 \pm \sqrt m \)

Bảng biến thiên

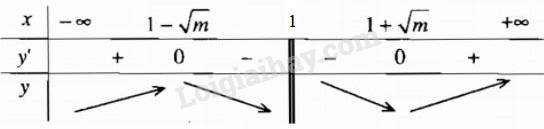
Hàm số nghịch biến trên mỗi khoảng \(\left( {1 - \sqrt m ;1} \right)\) và \(\left( {1;1 + \sqrt m } \right)\).

Điều kiện đòi hỏi không được thỏa mãn.

Vậy hàm số đồng biến trên mỗi khoảng xác định của nó khi và chỉ khi \(m \le 0\).