Bài 1.4 trang 10 SBT Giải tích 12 Nâng cao

Hãy chứng minh rằng

LG a

Hàm số \(y = \sqrt {2x - {x^2}} \) nghịch biến trên đoạn [1;2]

Lời giải chi tiết:

Hàm số liên tục trên đoạn [1;2] và có đạo hàm

\(y' = {{1 - x} \over {\sqrt {2x - {x^2}} }} < 0\) với mọi \(x \in (1,2)\)

Do đó hàm số nghịch biến trên đoạn [1;2]

LG b

Hàm số \(y = \sqrt {{x^2} - 9} \) đồng biến trên nửa khoảng  \({\rm{[}}3; + \infty )\)

Lời giải chi tiết:

Hàm số liên tục trên nửa khoảng  \({\rm{[}}3; + \infty )\) và có đạo hàm

\(y' = {x \over {\sqrt {{x^2} - 9} }} > 0\) với mọi \(x \in (3, + \infty )\)

Do đó hàm dố đồng biến tên nửa khoảng \({\rm{[}}3; + \infty )\)

LG c

Hàm số \(y = x + {4 \over x}\) nghịch biến trên mỗi nửa khoảng [-2;0) và (0;2]

Lời giải chi tiết:

TXĐ: \(x\ne0\)

\(y' = 1 - {4 \over {{x^2}}}\)

\(y' = 0 \Leftrightarrow x =  \pm 2\)

BBT

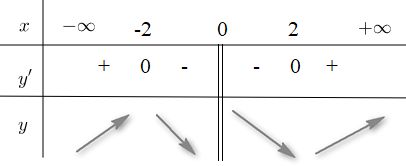
Từ BBT ta có hàm số \(y = x + {4 \over x}\) nghịch biến trên mỗi nửa khoảng [-2;0) và (0;2]