Bài 1.60 trang 18 SBT Đại số và Giải tích 11 Nâng cao
Giải bài 1.60 trang 18 sách bài tập Đại số và Giải tích 11 Nâng cao. Chứng minh rằng...
Đề bài
Chứng minh rằng
\({\cos ^2}(x - a) + {\sin ^2}(x - b) \)\(- 2\cos (x - a)\sin (x - b)\sin (a - b) \)\(= {\cos ^2}(a - b)\)
Lời giải chi tiết
Ta có:
\(\eqalign{
& {\cos ^2}(x - a) + {\sin ^2}(x - b) \cr&= {{1 + \cos 2\left( {x - a} \right)} \over 2} + {{1 - \cos 2\left( {x - b} \right)} \over 2} \cr
& = 1 + {1 \over 2}\left[ {\cos 2\left( {x - a} \right) - \cos 2\left( {x - b} \right)} \right] \cr& = 1 + \frac{1}{2}.\left( { - 2} \right)\sin \left( {2x - a - b} \right)\sin \left( {b - a} \right) \cr&= 1 - \sin \left( {2x - a - b} \right)\sin \left( {b - a} \right)\cr&= 1 + \sin \left( {2x - a - b} \right)\sin \left( {a - b} \right) \cr} \)
Do đó
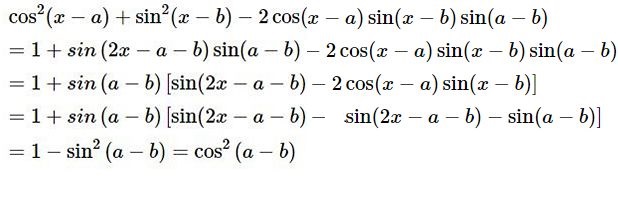
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.60 trang 18 SBT Đại số và Giải tích 11 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.60 trang 18 SBT Đại số và Giải tích 11 Nâng cao timdapan.com"







