Lý thuyết lôgarit

1. Định nghĩa

Cho hai số dương a, b với \(a\ne1\). Nghiệm duy nhất của phương trình \({a^x} = b\) được gọi là \({\log _a}b\) ( tức là số \(\alpha\) có tính chất là \({a^\alpha } = b\)).

Như vậy \({\log _a}b = \alpha  \Leftrightarrow {a^\alpha } = b\).

2. Loogarit thập phân và lôgarit tự nhiên

Trong đời sống và trog tự nhiên nghiên cứu, ta thường gặp và thường sử dụng loogarit thập phân và lôgarit tự nhiên.

Lôgarit cơ số 10 còn được gọi là lôgarit thập phân, số log₁₀b thường được viết là logb hoặc lgb.

Lôgarit cơ số \(e\) (\(e= \mathop {\lim }\limits_{n \to  + \infty } {\left( {1 + {1 \over n}} \right)^n}\) ≈ 2,718281828459045) còn được gọi là lôgarit tự nhiên, số log_eb thường được viết là lnb.

3. Tính chất của lôgarit

Lôgarit có các tính chất rất phong phú, có thể chia ra thành các nhóm sau đây.

1) Lôgarit của đơn vị và lôgarit của cơ số:

Với cơ số tùy ý, ta luôn có log_a1 = 0 và log_aa= 1.

2) Phép mũ hóa và phép lôgarit hóa theo cùng cơ số (mũ hóa số thực α theo cơ số a là tính a^α; lôgarit hóa số dương b theo cơ số a là tính log_ab) là hai phép toán ngược nhau.

∀a >0 (a\(\ne\) 1),  \(∀b> 0\), \({a^{{{\log }_a}b}} = b\) và \(∀a >0 (a\ne1)\), \({\log _a}{a^\alpha }= α\).

3) Lôgarit và các phép toán: Phép lôgarit hóa biến phép nhân thành phép cộng, phép chia thành phép trừ, phép nâng lên lũy thừa thành phép nhân, phép khai căn thành phép chia, cụ thể là 

Với \(\forall a,{b_1},{b_2} > 0,a \ne 1\) ta có:

+) \({\log _a}\left( {{b_1}{b_2}} \right) = {\log _a}{b_1} + {\log _a}{b_2}\)

+) \({\log _a}\left( {\dfrac{{{b_1}}}{{{b_2}}}} \right) = {\log _a}{b_1} - {\log _a}{b_2}\)

và \(∀a,b >0\) (a\(\ne\)1),  \(∀α\), \({\log _a}{b^\alpha } = \alpha {\log _a}b,{\log _a}\root n \of b  = {1 \over n}{\log _a}b\)

4) Đổi cơ số: Có thể chuyển các phép lấy lôgarit theo những cơ số khác nhau về việc tính lôgarit theo cùng một cơ số chung, cụ thể là 

\(∀a,b,c  >0\) (a, c\(\ne\)1), \({\log _a}b = {{{{\log }_c}b} \over {{{\log }_c}a}}\).

Đặc biệt \(∀a,b\) >0 (a,b \(\ne\)1) \({\log _a}b = {1 \over {{{\log }_b}a}}\)

và \(∀a,b >0\) (a\(\ne\)1),\( ∀α, β\) (\(α\ne 0\)), \({\log _{{a^\alpha }}}b = {1 \over \alpha }{\log _a}b,{\log _{{a^\alpha }}}{b^\beta } = {\beta  \over \alpha }{\log _a}b\)

4. Sử dụng máy tính cầm tay để tính lôgarit

Cũng giống như tính các lũy thừa, có thể sử dụng máy tính cầm tay để tính lôgarit. Để làm điều này, trước tiên các em phải bảo đảm máy tính đang làm việc trong môi trường tính toán bằng cách án các phím MODE, 1. Các máy CASIO fx-500 MS và CASIO fx-570 MS chỉ có chức năng tính trực tiếp các lôgarit thập phân và lôgarit tự nhiên, để tính các lôgarit cơ số khác, các em phải dùng công thức đổi cơ số để đưa bài toán về việc tính hai loại lôgarit đó. Máy CASIO fx-5770 ES, ngoài tính năng tính hai lại lôgarit vừa nói, còn có chức năng tính trực tiếp các lôgarit với cơ số tùy ý. Các em có thể học được cách sử dụng máy tính cầm tay để tính lôgarit qua tìm hiểu các ví dụ sau:

1) Tính log5,63 các em ấn liên tiếp; log, 5, ., 6, 3, màn hình hiện kết quả 0,750508395 (máy CASIO fx-500MS và CASIO fx- 570MS) hoặc 0,7505083949 (máy CASIO fx-50 ES).

2) Tính ln4,83 các em ấn liên tiếp: ln, 4, ., 8, 3, màn hình hiện thị kết quả 1.574846468 

3) Tính log₃5: 

- Dùng máy CASIO fx-500MS và CASIO fx-570 MS, các em cần đổi về lôgarit thập phân hoặc tự nhiên. Ta làm như sau: viết \({\log _3}5 = {{\ln 5} \over {\ln 3}}\) Từ đó ấn liên tiếp các phím ln, 5, 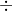, ln, 3, =. Màn hình hiện kết quả 1,464973521.

- Dùng máy CASIO fx-570 ES các em ấn các phím: log_□(□), 3, 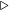, 5, =. Màn hình cũng hiện thị kết quả.