Bài 7 trang 46 SGK Giải tích 12

LG a

a) Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số: \(y = x^3+ 3x^2+ 1.\)

Phương pháp giải:

Khảo sát hàm số và vẽ đồ thị hàm số qua các bước đã học.

Lời giải chi tiết:

\(\displaystyle y = x^3+ 3x^2+ 1\)

Tập xác định: \(\displaystyle D =\mathbb R\)

* Sự biến thiên:

Ta có: \(\displaystyle y’= 3x^2+ 6x = 3x(x+ 2)\)

\(\displaystyle \begin{array}{l}
\Rightarrow y' = 0 \Leftrightarrow 3x\left( {x + 2} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x + 2 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = - 2
\end{array} \right..
\end{array}\)

- Hàm số đồng biến trên khoảng \(\displaystyle (-\infty;-2)\) và \(\displaystyle (0;+\infty)\), nghịch biến trên khoảng \(\displaystyle (-2;0)\)

- Cực trị:

Hàm số đạt cực đại tại \(\displaystyle x=-2\); \(\displaystyle y_{CĐ}=5\)

Hàm số đạt cực tiểu tại \(\displaystyle x=0\); \(\displaystyle y_{CT}=1\).

- Giới hạn: \(\displaystyle \mathop {\lim }\limits_{x \to - \infty } y = - \infty\), \(\displaystyle \mathop {\lim }\limits_{x \to + \infty } y = + \infty\)

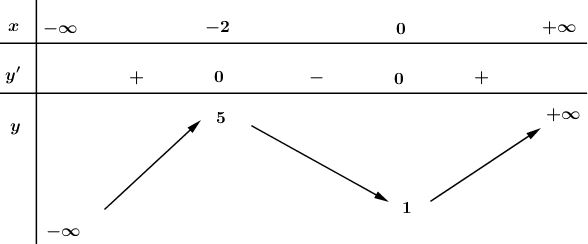
- Bảng biến thiên:

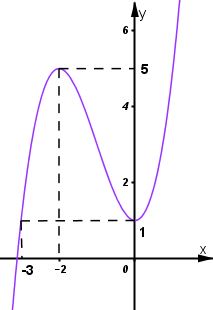
Đồ thị:

Đồ thị hàm số giao \(\displaystyle Oy\) tại \(\displaystyle (0;1)\)

Đồ thị hàm số nhận \(\displaystyle I(-1;3)\) làm tâm đối xứng.

LG b

b) Dựa vào đồ thị \((C)\), biện luận số nghiệm của phương trình sau theo \(m\): \({x^3} + 3{x^2} + 1 = {m \over 2}.\)

Phương pháp giải:

Số nghiệm của phương trình \(f(x) = \frac{m}{2}\) là số giao điểm của đồ thị hàm số \(y=f(x)\) và đường thẳng \(y=\frac{m}{2}.\) Dựa vào đồ thị để biện luận số nghiệm.

Lời giải chi tiết:

Số nghiệm của phương trình \(\displaystyle {x^3} + 3{x^2} + 1 = {m \over 2}\) chính là số giao điểm của \(\displaystyle (C)\) và đường thẳng \(\displaystyle (d)\): \(\displaystyle y = {m \over 2}\) 

Từ đồ thị ta thấy:

- Với \(\displaystyle {m \over 2} < 1 \Leftrightarrow m < 2\) : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm

- Với \(\displaystyle {m \over 2} = 1  ⇔ m = 2\): (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm.

- Với \(\displaystyle 1 < {m \over 2} < 5 ⇔ 2<m<10\): (d) cắt (C) tại 3 điểm, phương trình có 3 nghiệm.

- Với  \(\displaystyle {m \over 2} = 5 \Leftrightarrow m = 10\): (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.

- Với \(\displaystyle {m \over 2} > 5 \Leftrightarrow m > 10\): (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm.

Vậy, nếu \(m < 2\) hoặc \(m > 10\) thì phương trình có \(1\) nghiệm duy nhất.

+ Nếu \(m = 2\) hoặc \(m = 10\) thì phương trình có \(2\) nghiệm phân biệt.

+ Nếu \(2 < m < 10\) thì phương trình có \(3\) nghiệm phân biệt.

LG c

c) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị \((C).\)

Phương pháp giải:

Xác định tọa độ các điểm cực trị của hàm số. Sau đó sử dụng công thức sau để lập phương trình đường thẳng đi qua hai điểm \(A(x_A; \, y_A)\) và \(B(x_B; \, y_B):\)

\[\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}}.\]

Lời giải chi tiết:

Ta thấy hàm số có điểm cực đại là \(\displaystyle (-2, 5)\), điểm cực tiểu  là \(\displaystyle (0, 1)\). 

Đường thẳng đi qua hai điểm này có phương trình là: \(\displaystyle {{y - 1} \over 4} = {x \over { - 2}} \Leftrightarrow y =  - 2x + 1.\)