Bài 5 trang 45 SGK Giải tích 12

Cho hàm số \(y = 2x^2 + 2mx + m -1\) có đồ thị là \((C_m)\), \(m\) là tham số

LG a

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi \(m = 1\)

Phương pháp giải:

Khảo sát và vẽ đồ thị hàm số theo các bước đã được học.

Lời giải chi tiết:

\(y = 2x^2 + 2mx + m -1\) \((C_m)\). Đây là hàm số bậc hai, đồ thị là parabol quay bề lõm lên phía trên.

a) Với \(m = 1\) ta có hàm số: \(y = 2x^2+ 2x.\)

Tập xác định \(D =\mathbb R\)

* Sự biến thiên:

Ta có: \(y'=4x+2.\)
\(\Rightarrow y'=0 \Leftrightarrow  4x + 2 = 0 \Leftrightarrow x = -{{  1} \over 2} \)

+) Hàm số đồng biến trên khoảng \((-{1\over2};+\infty)\), nghịch biến trên khoảng \((-\infty; -{1\over2})\)

+) Cực trị:

    Hàm số đạt cực tiểu tại \(x=-{1\over2}\); \(y_{CT}=-{1\over 2}\)

+) Giới hạn:

   \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \)

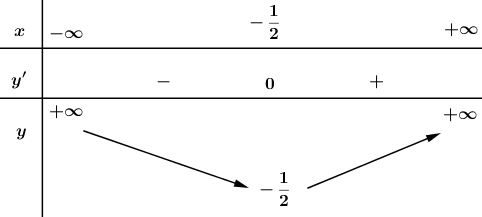
Bảng biến thiên:

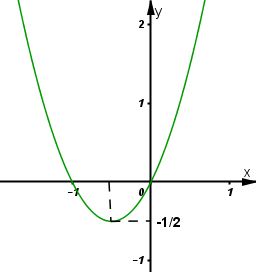
*Đồ  thị

Đồ thị hàm số giao trục \(Ox\) tại hai điểm \((-1;0)\) và \((0;0)\)

LG b

b) Xác định m để hàm số:

- Đồng biến trên khoảng \((-1, +∞)\)

- Có cực trị trên khoảng \((-1, +∞)\)

Phương pháp giải:

Hàm số đồng biến trên \( (a; \, b)  \Leftrightarrow y' \ge 0\;\;\forall x \ne \left( {a;\;b} \right).\) 

+) Hàm số đồng biến trên \( (a; \, b)  \Leftrightarrow y' \le 0\;\;\forall x \ne \left( {a;\;b} \right).\) 

Lời giải chi tiết:

Tổng quát \(y = 2x^2+ 2mx + m -1\) có tập xác định \(D = \mathbb R\)

 Có \(y' = 4x + 2m = 0 \Rightarrow y'=0 \)

\(\Leftrightarrow 4x+2m=0 \Leftrightarrow x = -{{  m} \over 2}\)

Suy ra \(y’ >\) 0 với \(x > -{{  m} \over 2};y' < 0\) với \(x < -{{  m} \over 2}\) , tức là hàm số nghịch biến trên \(( - \infty ;-{{  m} \over 2})\) và đồng biến trên \((-{{ m} \over 2}; + \infty )\)

i) Để hàm số đồng biến trên khoảng \((-1, +∞)\) thì phải có điều kiện \(( - 1;{\rm{ }} + \infty )  \subset  (-{{  m} \over 2}; + \infty )\)

  \( \Leftrightarrow -{{ m} \over 2} \le  - 1 \Leftrightarrow m \ge 2\)

ii) Hàm số đạt cực trị tại  \(x = -{{  m} \over 2}\) .

Để hàm số đạt cực trị trong khoảng \((-1; +∞)\), ta phải có:

\(\eqalign{
& {{ - m} \over 2} \in ( - 1, + \infty ) \cr 
& \Leftrightarrow -{{  m} \over 2} > - 1 \Leftrightarrow 1 > {m \over 2} \Leftrightarrow m < 2 \cr} \)

LG c

c) Chứng minh rằng \((C_m)\) luôn cắt trục hoành tại hai điểm phân biệt với mọi \(m\).

Phương pháp giải:

Đồ thị hàm số \((C_m)\) cắt trục hoành tại hai điểm phân biệt với mọi \(m \Leftrightarrow y=f(x)=0\) có hai nghiệm phân biệt với mọi \(m.\)

Lời giải chi tiết:

\((C_m)\) luôn cắt \(Ox\) tại hai điểm phân biệt \(x = -{{ m} \over 2}\)

\(⇔\) phương trình \(2x^2+ 2mx + m – 1 = 0\) có hai nghiệm phân biệt.

Ta có: \(Δ’ = m^2– 2m + 2 = (m-1)^2+ 1 > 0 ∀m\)

Vậy \((C_m)\) luôn cắt \(O x\) tại hai điểm phân biệt.