Bài 6 trang 45 SGK Giải tích 12

LG a

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số \((C)\) của hàm số \(f(x)  = - {x^3} + 3{x^2} + 9x + 2.\)

Phương pháp giải:

Khảo sát và vẽ đồ thị hàm số qua các bước đã học.

Lời giải chi tiết:

Tập xác định: \(D =\mathbb R\)

* Sự biến thiên:  

Ta có:\( y' = - 3{x^2} + 6x + 9.\)

\( \Rightarrow y'=0  \Leftrightarrow - 3{x^2} + 6x + 9 = 0   \)

\(\begin{array}{l}
\Leftrightarrow - 3\left( {x + 1} \right)\left( {x - 3} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x + 1 = 0\\
x - 3 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - 1\\
x = 3
\end{array} \right..
\end{array}\)

- Hàm số đồng biến trên khoảng: \((-1;3)\), nghịch biến trên khoảng \((-\infty; -1)\) và \((3;+\infty)\)

- Cực trị:

    Hàm số đạt cực đại tại \(x=3\); \(y_{CĐ}=29\)

    Hàm số đạt cực tiểu tại \(x=-1\); \(y_{CT}=-3\)

- Giới hạn:

   \(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty\)
   \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \)

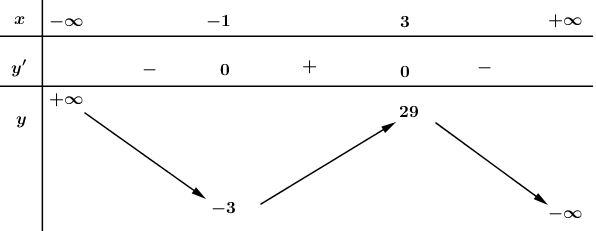
-Bảng biến thiên:

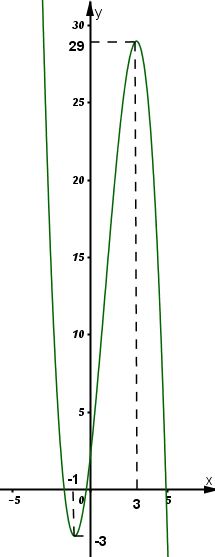
* Đồ thị

Đồ thị hàm số giao trục \(Oy\) tại điểm \((0;2)\)

Đồ thị hàm số nhận \(I(1;13)\) làm tâm đối xứng.

LG b

b) Giải bất phương trình \(f’(x-1)>0.\)

Phương pháp giải:

Tính đạo hàm \(y=f'(x).\) Thay \(x-1\) vào vị trí của \(x\) để tính \(f'(x-1)\) và giải bất phương trình \(f'(x-1)>0.\)

Lời giải chi tiết:

\(y=f(x) = f(x)  = - {x^3} + 3{x^2} + 9x + 2\)

\(f’(x) = - 3{x^2} + 6x + 9 = 0\). 

\( \Rightarrow f’(x-1)=-3(x-1)^2+6(x-1)+9\)

= \(-3x^2+ 12x = -3x(x-4) \)

\( \Rightarrow f'(x-1)> 0 ⇔  -3x(x-4) >0 \) \(⇔x(x-4)<0⇔0<x

LG c

c) Viết phương trình tiếp tuyến của đồ thị \((C)\) tại điểm có hoành độ \(x_0,\) biết rằng \(f’’(x_0) = -6.\)

Phương pháp giải:

Giải phương trình \(f''(x_0)=-6\) để tìm \(x_0.\) Sau đó viết phương trình tiếp tuyến của đồ thị hàm số \((C)\) theo công thức: \(y=y'(x_0)(x-x_0)+y(x_0).\)

Lời giải chi tiết:

Có \(f’’(x) = -6x+6\)

\(f’’(x_0)= -6 ⇔ -6x_0+ 6 = -6 ⇔ x_0= 2\)

Do đó: \(f’(2) = 9, f(2) = 24\).

Phương trình tiếp tuyến của \((C)\) tại \(x_0= 2\) là:

\(y=f’(2)(x-2) + f(2)  ⇔  y=9(x-2) +24 \) \(⇔y = 9x+6.\)