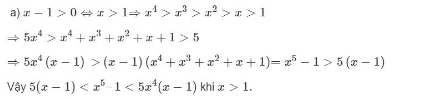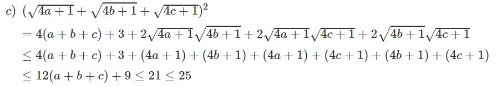Bài 4 trang 160 SGK Đại số 10

Chứng minh các bất đẳng thức:

LG a

\(5(x-1) < x^5– 1< 5x^4(x-1)\), biết \(x – 1 > 0\)

Lời giải chi tiết:

LG b

\(x^5+ y^5– x^4y – xy^4≥ 0\), biết \(x + y ≥ 0\)

Lời giải chi tiết:

\(\begin{array}{l}
{x^5} + {y^5} - {x^4}y - x{y^4}\\
= \left( {{x^5} - {x^4}y} \right) - \left( {x{y^4} - {y^5}} \right)\\
= {x^4}\left( {x - y} \right) - {y^4}\left( {x - y} \right)\\
= \left( {x - y} \right)\left( {{x^4} - {y^4}} \right)\\
= \left( {x - y} \right)\left( {{x^2} - {y^2}} \right)\left( {{x^2} + {y^2}} \right)\\
= \left( {x - y} \right)\left( {x - y} \right)\left( {x + y} \right)\left( {{x^2} + {y^2}} \right)\\
= {\left( {x - y} \right)^2}\left( {x + y} \right)\left( {{x^2} + {y^2}} \right)
\end{array}\)

Vì 

\(\left\{ \begin{array}{l}
{\left( {x - y} \right)^2} \ge 0\\
x + y \ge 0\\
{x^2} + {y^2} \ge 0
\end{array} \right.\)

nên \({\left( {x - y} \right)^2}\left( {x + y} \right)\left( {{x^2} + {y^2}} \right) \ge 0\)

Hay ta có đpcm.

LG c

\(\sqrt {4a + 1}  + \sqrt {4b + 1}  + \sqrt {4c + 1}  < 5\), biết rằng \(a, b, c\)  cùng lớn hơn \( - \dfrac{1}{4}\) và  \(a + b + c = 1.\)

Phương pháp giải:

Áp dụng bất đẳng thức Cô si: \(a + b \ge 2\sqrt {ab}  \Leftrightarrow \sqrt {ab}  \le \dfrac{{a + b}}{2}\)

Lời giải chi tiết:

Cách khác:

Với 

\(a,b,c > - \dfrac{1}{4} \Rightarrow \left\{ \begin{array}{l}
4a + 1 > 0\\
4b + 1 > 0\\
4c + 1 > 0
\end{array} \right.\)

Áp dụng bất đẳng thức Cô si ta có:

\(\sqrt {4a + 1}  = \sqrt {\left( {4a + 1} \right).1} \)\( \le \dfrac{{\left( {4a + 1} \right) + 1}}{2} = 2a + 1\)

\(\sqrt {4b + 1}  = \sqrt {\left( {4b + 1} \right).1} \)\( \le \dfrac{{\left( {4b + 1} \right) + 1}}{2} = 2b + 1\)

\(\sqrt {4c + 1}  = \sqrt {\left( {4c + 1} \right).1} \)\( \le \dfrac{{\left( {4c + 1} \right) + 1}}{2} = 2c + 1\)

Cộng vế với vế các bđt trên ta được:

\(\sqrt {4a + 1}  + \sqrt {4b + 1}  + \sqrt {4c + 1} \) \( \le \left( {2a + 1} \right) + \left( {2b + 1} \right) + \left( {2c + 1} \right)\)

\( = 2a + 2b + 2c + 3\) \( = 2\left( {a + b + c} \right) + 3\) \( = 2.1 + 3 = 5\)

\( \Rightarrow \sqrt {4a + 1}  + \sqrt {4b + 1}  + \sqrt {4c + 1}  \le 5\)

Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}4a + 1 = 1\\4b + 1 = 1\\4c + 1 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\\c = 0\end{array} \right.\) (không thỏa mãn \(a + b + c = 1\))

Vậy dấu “=” không xảy ra hay \(\sqrt {4a + 1}  + \sqrt {4b + 1}  + \sqrt {4c + 1}  < 5\).

Suy ra ĐPCM.

Cách khác:

Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}4a + 1 = 1\\4b + 1 = 1\\4c + 1 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\\c = 0\end{array} \right.\) (không thỏa mãn \(a + b + c = 1\))

Vậy dấu “=” không xảy ra hay \(\sqrt {4a + 1}  + \sqrt {4b + 1}  + \sqrt {4c + 1}  < 5\).

Suy ra ĐPCM.