Bài 3 trang 94 SGK Toán 11 tập 1 - Cánh diều
Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.
Đề bài
Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.
Phương pháp giải - Xem chi tiết
Dùng phản chứng: Giả sử ba đường thẳng không đồng quy. Chứng minh điều giả sử là sai.
Lời giải chi tiết
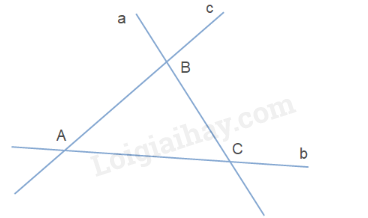
Giả sử:
Đường thẳng a và b cắt nhau tại C
Đường thẳng a và c cắt nhau tại B
Đường thẳng b và c cắt nhau tại A
Trong đó: A, B, C không đồng quy (*)
Khi đó: B và C thuộc đường thẳng a
Mặt khác: B thuộc đường thẳng c, C thuộc đường thẳng b
Suy ra: BC thuộc mp chứa đường thẳng b và c
Do đó: Đường thẳng a thuộc mp (b,c) nên ba đường thẳng này đồng quy (mâu thuẫn với (*)).
Vậy ba đường thẳng a, b, c cùng đi qua một điểm.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 94 SGK Toán 11 tập 1 - Cánh diều timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 94 SGK Toán 11 tập 1 - Cánh diều timdapan.com"







