Câu hỏi 1 trang 32 SGK Giải tích 12

Đề bài

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số đã học theo sơ đồ trên.

Lời giải chi tiết

y = ax + b

y = ax² + bx + c

Lời giải:

* Hàm số y = ax + b

Trường hợp a > 0

1. TXĐ: D = R.

2. Sự biến thiên.

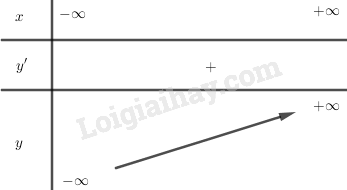
y’ = a > 0. Vậy hàm số đồng biến trên toàn bộ R.

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr
& \mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr} \)

Bảng biến thiên

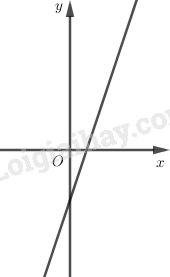
3. Vẽ đồ thị

Trường hợp a < 0

1. TXĐ: D = R.

2. Sự biến thiên.

y’ = a < 0. Vậy hàm số đồng biến trên toàn bộ R.

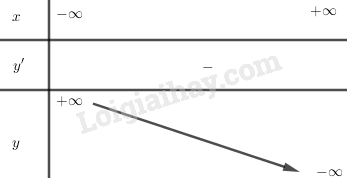
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr
& \mathop {\lim }\limits_{x \to - \infty } y = + \infty \cr} \)

Bảng biến thiên

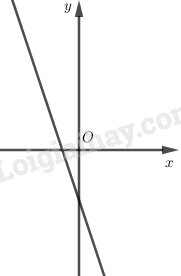
Vẽ đồ thị

* Hàm số y = ax2 + bx + c

Trường hợp a > 0

1. TXĐ: D = R.

2. Sự biến thiên.

y’ = 2ax + b. 

\(y' = 0 \Rightarrow x = {{ - b} \over {2a}}\)

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr 
& \mathop {\lim }\limits_{x \to - \infty } y = + \infty \cr} \)

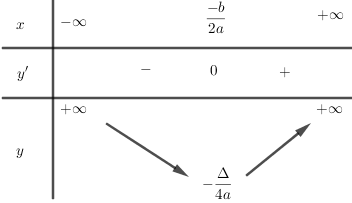
Bảng biến thiên

Hàm số nghịch biến trên khoảng (-∞, \({{ - b} \over {2a}}\)).

Hàm số đồng biến trên khoảng [\({{ - b} \over {2a}}\), +∞].

Hàm số đạt cực tiểu bằng \( - {\Delta  \over {4a}}\) tại x = \({{ - b} \over {2a}}\)

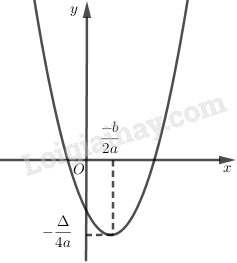
Vẽ đồ thị

Trường hợp a < 0

1. TXĐ: D = R.

2. Sự biến thiên.

y’ = 2ax + b. 

Cho \(y' = 0 \Rightarrow x = {{ - b} \over {2a}}\)

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr} \)

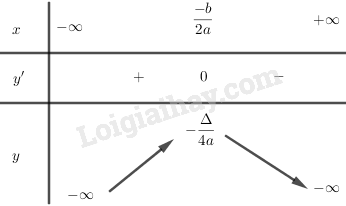
Bảng biến thiên

Hàm số đồng biến trên khoảng (-∞, \({{ - b} \over {2a}}\)).

Hàm số nghịch biến trên khoảng \([{{ - b} \over {2a}}, +∞]\).

Hàm số đạt cực đại bằng \( - {\Delta  \over {4a}}\) tại x = \({{ - b} \over {2a}}\)

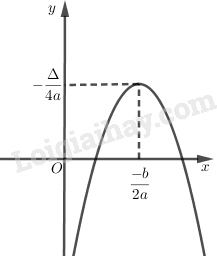
Vẽ đồ thị