Bài 3 trang 43 SGK Giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số phân thức:2696

LG a

\(\displaystyle {{x + 3} \over {x - 1}}\),

Phương pháp giải:

Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:

Bước 1: Tìm TXĐ của hàm số.

Bước 2: Khảo sát sự biến thiên:

*) Xét chiều biến thiên của hàm số:

+) Tính đạo hàm.

+) Tìm các điểm \({{x}_{i}}\) mà tại đó đạo hàm có \(y'=0\) hoặc đạo hàm không xác định.

+) Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.

*) Tìm cực trị: \(y\left( {{x}_{i}} \right).\)

*) Tìm các giới hạn vô cực, các giới hạn có kết quả là vô cực và tiệm cận của đồ thị hàm số (nếu có): \(\mathop {\lim }\limits_{x \to  \pm \infty } y,\mathop {\lim }\limits_{x \to {x_0}} y,...\)

*) Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

Bước 3: Đồ thị:

+) Giao điểm của đồ thị với trục tung: \(x=0\Rightarrow y=....\Rightarrow A\left( 0;\ ..... \right).\)

+) Giao điểm của đồ thị với trục hoành: \(y=0\Rightarrow x=.....\Rightarrow B\left( ...;0 \right).\)

+) Các điểm cực đại, cực tiểu nếu có.

Lời giải chi tiết:

Tập xác định : \(\displaystyle \mathbb R{\rm{\backslash \{ }}1\}\);  

* Sự biến thiên:

Ta có: \(\displaystyle y' = {{ - 4} \over {{{(x - 1)}^2}}} < 0,\forall x \ne 1\) ;

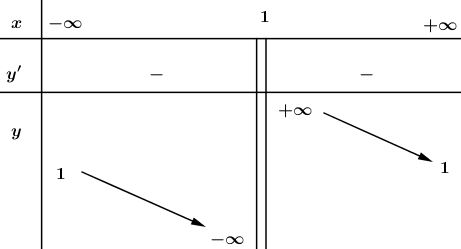
- Hàm số nghịch biến trên khoảng: \(\displaystyle (-\infty;1)\) và \(\displaystyle (1;+\infty)\).

- Cực trị:

 Hàm số không có cực trị.

- Tiệm cận:

\(\displaystyle \mathop {\lim y}\limits_{x \to {1^ - }}  =  - \infty \), \(\displaystyle \mathop {\lim y}\limits_{x \to {1^ + }}  =  +\infty\); \(\displaystyle \mathop {\lim y}\limits_{x \to  \pm \infty }  = 1\)

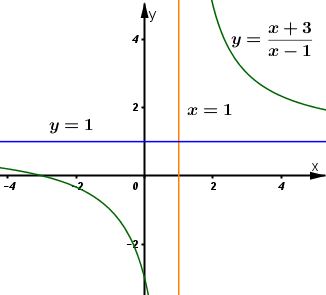
Do đó, tiệm cận đứng là: \(\displaystyle x = 1\); tiệm cận ngang là: \(\displaystyle y = 1\).

Bảng biến thiên: 

* Đồ thị:

Đồ thị nhận điểm \(\displaystyle I(1;1)\) làm tâm đối xứng.

Đồ thị giao trục tung tại:\(\displaystyle (0;-3)\), trục hoành tại \(\displaystyle (-3;0)\)

LG b

\(\displaystyle {{1 - 2{\rm{x}}} \over {2{\rm{x}} - 4}}\),

Phương pháp giải:

Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:

Bước 1: Tìm TXĐ của hàm số.

Bước 2: Khảo sát sự biến thiên:

*) Xét chiều biến thiên của hàm số:

+) Tính đạo hàm.

+) Tìm các điểm \({{x}_{i}}\) mà tại đó đạo hàm có \(y'=0\) hoặc đạo hàm không xác định.

+) Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.

*) Tìm cực trị: \(y\left( {{x}_{i}} \right).\)

*) Tìm các giới hạn vô cực, các giới hạn có kết quả là vô cực và tiệm cận của đồ thị hàm số (nếu có): \(\mathop {\lim }\limits_{x \to  \pm \infty } y,\mathop {\lim }\limits_{x \to {x_0}} y,...\)

*) Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

Bước 3: Đồ thị:

+) Giao điểm của đồ thị với trục tung: \(x=0\Rightarrow y=....\Rightarrow A\left( 0;\ ..... \right).\)

+) Giao điểm của đồ thị với trục hoành: \(y=0\Rightarrow x=.....\Rightarrow B\left( ...;0 \right).\)

+) Các điểm cực đại, cực tiểu nếu có.

Lời giải chi tiết:

Tập xác định : \(\displaystyle \mathbb R \backslash {\rm{\{ }}2\} \);    

* Sự biến thiên:

Ta có: \(\displaystyle y' = {6 \over {{{\left( {2{\rm{x}} - 4} \right)}^2}}} > 0,\forall x \ne 2\)

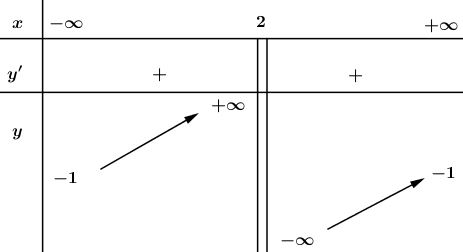
- Hàm số đồng biến trên khoảng: \(\displaystyle (-\infty;2)\) và \(\displaystyle (2;+\infty)\)

- Cực trị: 

 Hàm số không có cực trị.

- Tiệm cận:

\(\displaystyle \mathop {\lim y}\limits_{x \to {2^ - }}  =  + \infty \), \(\displaystyle \mathop {\lim y}\limits_{x \to {2^ + }}  =  - \infty \), \(\displaystyle \mathop {\lim y}\limits_{x \to  \pm \infty }  =  - 1\)

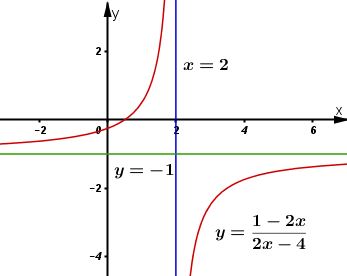
Do đó, tiệm cận đứng là: \(\displaystyle x = 2\); tiệm cận ngang là:\(\displaystyle y = -1\).

Bảng biến thiên :

* Đồ thị:

Đồ thị nhận điểm \(\displaystyle I(2;-1)\) lầm tâm đối xứng.

Đồ thị giao trục tung tại: \(\displaystyle \left( {0; - {1 \over 4}} \right)\), trục hoành tại: \(\displaystyle \left( {{1 \over 2};0} \right)\)

LG c

\(\displaystyle {{ - x + 2} \over {2{\rm{x}} + 1}}\)

Phương pháp giải:

Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:

Bước 1: Tìm TXĐ của hàm số.

Bước 2: Khảo sát sự biến thiên:

*) Xét chiều biến thiên của hàm số:

+) Tính đạo hàm.

+) Tìm các điểm \({{x}_{i}}\) mà tại đó đạo hàm có \(y'=0\) hoặc đạo hàm không xác định.

+) Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.

*) Tìm cực trị: \(y\left( {{x}_{i}} \right).\)

*) Tìm các giới hạn vô cực, các giới hạn có kết quả là vô cực và tiệm cận của đồ thị hàm số (nếu có): \(\mathop {\lim }\limits_{x \to  \pm \infty } y,\mathop {\lim }\limits_{x \to {x_0}} y,...\)

*) Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

Bước 3: Đồ thị:

+) Giao điểm của đồ thị với trục tung: \(x=0\Rightarrow y=....\Rightarrow A\left( 0;\ ..... \right).\)

+) Giao điểm của đồ thị với trục hoành: \(y=0\Rightarrow x=.....\Rightarrow B\left( ...;0 \right).\)

+) Các điểm cực đại, cực tiểu nếu có.

Lời giải chi tiết:

Tập xác định : \(\displaystyle R\backslash \left\{ { - {1 \over 2}} \right\}\);

Sự biến thiên:

Ta có: \(\displaystyle y' = {{ - 5} \over {{{\left( {2{\rm{x}} + 1} \right)}^2}}} < 0,\forall x \ne  - {1 \over 2}\)

- Hàm số nghịch biến trên khoảng: \(\displaystyle (-\infty;{-1\over 2})\) và \(\displaystyle ({-1\over 2};+\infty)\)

- Cực trị:

Hàm số không có cực trị.

- Tiệm cận:

\(\displaystyle \mathop {\lim y}\limits_{x \to  - {{{1 \over 2}}^ - }}  =  - \infty \), \(\displaystyle \mathop {\lim y}\limits_{x \to  - {{{1 \over 2}}^ + }}  =  + \infty \), \(\displaystyle \mathop {\lim y}\limits_{x \to  \pm \infty }  =  - {1 \over 2}\)

Do đó, tiệm cận đứng là: \(\displaystyle x =  - {1 \over 2}\); tiệm cận ngang là: \(\displaystyle y =  - {1 \over 2}\).

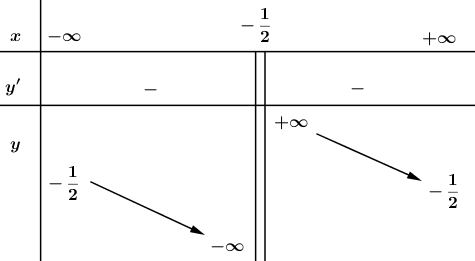
Bảng biến thiên :

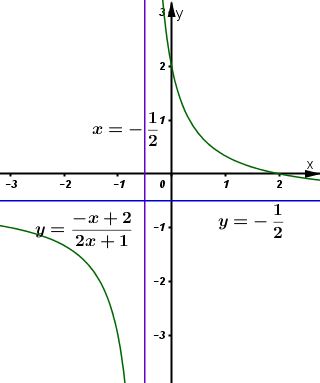
* Đồ thị    

Đồ thị nhận điểm \(\displaystyle I( - {1 \over 2}; - {1 \over 2})\) làm tâm đối xứng.

Đồ thị giao \(\displaystyle Ox\) tại: \(\displaystyle (2;0)\), \(\displaystyle Oy\) tại: \(\displaystyle (0;2)\)