Bài 9 trang 44 SGK Giải tích 12

Cho hàm số \(y=\frac{(m+1)x-2m+1}{x-1}\) (m là tham số) có đồ thị là \((G)\).

LG a

a) Xác định \(m\) để đồ thị \((G)\) đi qua điểm \((0 ; -1)\).

Phương pháp giải:

Thay tọa độ điểm đề bài đã cho vào công thức hàm số để tìm m.

Lời giải chi tiết:

Theo đề bài ta có \((0 ; -1) ∈ (G) \) \(⇔ -1=\dfrac{(m+1)\cdot 0-2m+1}{0-1}\) \(\Leftrightarrow m=0.\)

LG b

b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với \(m\) tìm được.

Phương pháp giải:

Thay giá trị m đã tìm được ở câu a vào đồ thị hàm số sau đó khảo sát và vẽ đồ thị hàm số.

Lời giải chi tiết:

Với \(m = 0\) ta được hàm số \(y=\dfrac{x+1}{x-1}\)  (G₀).

Tập xác định: \(D=\mathbb R \backslash {\rm{\{ }}1\}\)

* Sự biến thiên: 

Ta có: \(y' = {{ - 2} \over {{{(x - 1)}^2}}} < 0\forall x \in D\)

- Hàm số nghịch biến trên khoảng: \((-\infty;1)\) và \((1;+\infty)\).

- Cực trị:

    Hàm số không có cực trị.

- Tiệm cận:

    \(\eqalign{
& \mathop {\lim y}\limits_{x \to \pm \infty } = 1 \cr 
& \mathop {\lim y}\limits_{x \to {1^ - }} = - \infty \cr 
& \mathop {\lim y}\limits_{x \to {1^ + }} = + \infty \cr} \)

Tiệm cận đứng là: \(x=1\), tiệm cận ngang là: \(y=1\)

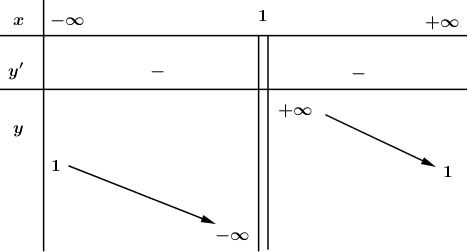
- Bảng biến thiên:

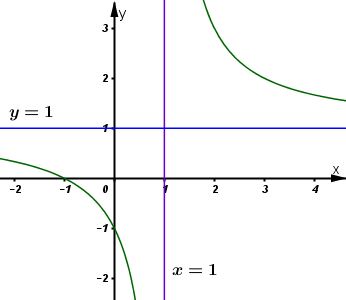
* Đồ thị:

Đồ thị hàm số giao trục \(Ox\) tại \((-1;0)\), trục \(Oy\) tại \((0;-1)\)

Đồ thị hàm số nhận \(I(1;1)\) làm tâm đối xứng.

LG c

c) Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung.

Phương pháp giải:

Đồ thị hàm số cắt trục tung tại điểm có M tung độ  \(y = y_0 \Rightarrow M(0;y_0) \).

+) Viết phương trình tiếp tuyến của đồ thị hàm số tại  \(M\left( {{x_0};{y_0}} \right)\) bằng công thức:  \(y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\).

Lời giải chi tiết:

(G₀) cắt trục tung tại \(M(0 ; -1)\).

\(y'=\dfrac{-2}{(x-1)^{2}}\Rightarrow y'(0) = -2\).

Phương trình tiếp tuyến của (G₀) tại \(M\) là: \(y - (-1) = y'(0)(x - 0) \) \(⇔ y= -2x - 1\)