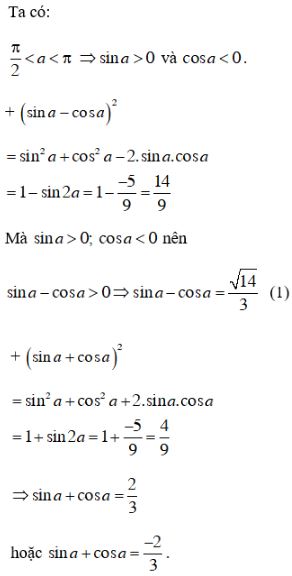Bài 6 trang 154 SGK Đại số 10

Giải bài 6 trang 154 SGK Đại số 10. Tính sina và cosa.

Đề bài

Cho \(\displaystyle \sin 2a = - {5 \over 9}\) và \(\displaystyle {\pi \over 2} < a < π\).

Tính \(\displaystyle \sin a\) và \(\displaystyle \cos a.\)

Phương pháp giải - Xem chi tiết

+) Với \(\dfrac{{\pi }}{2} < a < \pi\) ta có \(\sin a > 0, \, \, \cos a < 0.\)

+) \(\sin^2 \alpha +\cos^2 \alpha =1. \)

+) \(\sin 2a = 2\sin a.\cos a.\)

+) \(\cos 2a = {\cos ^2}a - {\sin ^2}a \) \(= 2{\cos ^2}a - 1\)\( = 1 - 2{\sin ^2}a.\)

+) \(\sin^2 a = \dfrac{{1 - \cos 2a}}{2}.\)

+) \(\cos^2 a = \dfrac{{1 + \cos 2a}}{2}.\)

Lời giải chi tiết

Với \(\displaystyle {\pi \over 2}< a < π\Rightarrow \sin a > 0, \cos a < 0.\)

\(\displaystyle \begin{array}{l}
{\sin ^2}2a + {\cos ^2}2a = 1\\
\Rightarrow {\cos ^2}2a = 1 - {\sin ^2}2a\\
= 1 - {\left( {\dfrac{5}{9}} \right)^2} = \dfrac{{56}}{{81}}\\
\Rightarrow \cos 2a = \pm \sqrt {\dfrac{{56}}{{81}}} = \pm \dfrac{{2\sqrt {14} }}{9}
\end{array}\)

Nếu \(\displaystyle \cos 2a = {{2\sqrt {14} } \over 9}\) thì

\(\displaystyle {\sin ^2}a = \frac{{1 - \cos 2a}}{2}\)

\(\displaystyle \eqalign{
& \Rightarrow \sin a = \sqrt {{{1 - \cos 2a} \over 2}} = \sqrt {{{1 - {{2\sqrt {14} } \over 9}} \over 2}} \cr&= {{\sqrt {9 - 2\sqrt {14} } } \over {3\sqrt 2 }} = {{\sqrt {{{\left( {\sqrt 7 - \sqrt 2 } \right)}^2}} } \over {3\sqrt 2 }}\cr& = {{\sqrt 7 - \sqrt 2 } \over {3\sqrt 2 }} = {{\sqrt {14} - 2} \over 6} \cr} \)

\(\displaystyle {\cos ^2}a = \frac{{1 + \cos 2a}}{2}\) \(\displaystyle \Rightarrow \cos a = - \sqrt {{{1 + \cos 2a} \over 2}} \) \(\displaystyle = - \sqrt {\frac{{1 + \frac{{2\sqrt {14} }}{9}}}{2}} \) \(\displaystyle = - \sqrt {\frac{{9 + 2\sqrt {14} }}{{18}}} \) \(\displaystyle = - \frac{{\sqrt {{{\left( {\sqrt 7 + \sqrt 2 } \right)}^2}} }}{{\sqrt {18} }}\) \(\displaystyle = - \frac{{\sqrt 7 + \sqrt 2 }}{{3\sqrt 2 }} \) \(\displaystyle = - \frac{{\sqrt {14} + 2}}{6}\)

Nếu \(\displaystyle \cos 2a = -{{2\sqrt {14} } \over 9}\) thì

\(\displaystyle {\sin ^2}a = \frac{{1 - \cos 2a}}{2}\)

\(\displaystyle \eqalign{
& \Rightarrow \sin a = \sqrt {{{1 - \cos 2a} \over 2}} = \sqrt {{{1 + {{2\sqrt {14} } \over 9}} \over 2}} \cr&= {{\sqrt {9 + 2\sqrt {14} } } \over {3\sqrt 2 }} = {{\sqrt {{{\left( {\sqrt 7 + \sqrt 2 } \right)}^2}} } \over {3\sqrt 2 }}\cr& = {{\sqrt 7 + \sqrt 2 } \over {3\sqrt 2 }} = {{\sqrt {14} + 2} \over 6} \cr } \)

\(\displaystyle {\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)

\(\displaystyle \Rightarrow \cos a = - \sqrt {{{1 + \cos 2a} \over 2}} \) \(\displaystyle = - \sqrt {\frac{{1 - \frac{{2\sqrt {14} }}{9}}}{2}} \) \(\displaystyle = - \sqrt {\frac{{9 - 2\sqrt {14} }}{{18}}} \) \(\displaystyle = - \frac{{\sqrt {{{\left( {\sqrt 7 - \sqrt 2 } \right)}^2}} }}{{\sqrt {18} }}\) \(\displaystyle = - \frac{{\sqrt 7 - \sqrt 2 }}{{3\sqrt 2 }} \) \(\displaystyle = - \frac{{\sqrt {14} - 2}}{6}\)

Cách khác: