Bài 2.79 trang 108 SBT hình học 10
Giải bài 2.79 trang 108 sách bài tập hình học 10. Cho tam giác...
Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), \(AB = a\), \(BC = 2a\). Tích vô hướng \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng
A. \({a^2}\)
B. \( - {a^2}\)
C. \(\dfrac{1}{2}{a^2}\)
D. \({a^2}\sqrt 3 \)
Phương pháp giải - Xem chi tiết
Tính \(\cos B\) và áp dụng công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\) tính tích vô hướng.
Lời giải chi tiết
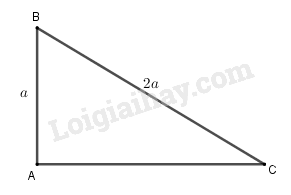
Ta có: \(\Delta ABC\) vuông tại \(A\) nên \(\cos B = \dfrac{{AB}}{{BC}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\)
\(\overrightarrow {BA} .\overrightarrow {BC} \)\( = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\) \( = a.2a.\dfrac{1}{2} = {a^2}\).
Chọn A.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.79 trang 108 SBT hình học 10 timdapan.com"







