Bài 2.76 trang 107 SBT hình học 10

Đề bài

Gọi \(G\) là trọng tâm tam giác đều \(ABC\) có cạnh bằng \(a\). Trong các khẳng định sau, tìm khẳng định sai:

A. \(\overrightarrow {AB} .\overrightarrow {AC}  = \dfrac{1}{2}{a^2}\)

B. \(\overrightarrow {AC} .\overrightarrow {CB}  =  - \dfrac{1}{2}{a^2}\)

C. \(\overrightarrow {GA} .\overrightarrow {GB}  = \dfrac{{{a^2}}}{6}\)

D. \(\overrightarrow {AB} .\overrightarrow {AG}  = \dfrac{1}{2}{a^2}\)

Lời giải chi tiết

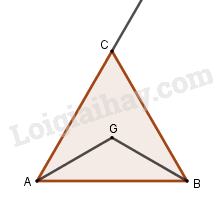
Đáp án A: \(\overrightarrow {AB} .\overrightarrow {AB} \) \( = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\) \( = a.a.\cos {60^0} = \dfrac{1}{2}{a^2}\)

A đúng.

Đáp án B: \(\overrightarrow {AC} .\overrightarrow {CB} \)\( = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)\) \( = a.a.\cos {120^0} =  - \dfrac{1}{2}{a^2}\)

B đúng.

Đáp án C: Tam giác \(ABC\) đều nên chiều cao \(AH = \dfrac{{a\sqrt 3 }}{2}\) và \(AG = \dfrac{2}{3}AH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).

Do đó \(\overrightarrow {GA} .\overrightarrow {GB} \) \( = \left| {\overrightarrow {GA} } \right|.\left| {\overrightarrow {GB} } \right|.\cos \left( {\overrightarrow {GA} ,\overrightarrow {GB} } \right)\) \( = \dfrac{{a\sqrt 3 }}{3}.\dfrac{{a\sqrt 3 }}{3}.\cos {120^0} =  - \dfrac{{{a^2}}}{6}\)

C sai.

Chọn C.