Bài 6 trang 27 (Ôn tập chương I - Vectơ) SGK Hình học 10

Cho tam giác đều \(ABC\) có cạnh bằng \(a\). Tính:

LG a

 \(|\overrightarrow {AB}  + \overrightarrow {AC} |\)

Lời giải chi tiết:

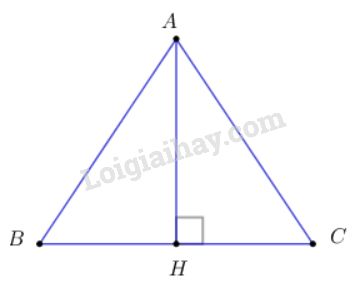
Hạ \(AH\bot BC\) do tam giác \(ABC\) đều nên \(H\) là trung điểm của \(BC\)

Ta có:

\(\eqalign{
& \overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AH} \cr 
& \Rightarrow |\overrightarrow {AB} + \overrightarrow {AC} | = 2|\overrightarrow {AH} | = 2AH \cr} \)

Mà \(AH = {{a\sqrt 3 } \over 2} \Rightarrow |\overrightarrow {AB}  + \overrightarrow {AC} | = a\sqrt 3 \)

LG b

\(|\overrightarrow {AB}  - \overrightarrow {AC} |\)

Lời giải chi tiết:

\(|\overrightarrow {AB}  - \overrightarrow {AC} | = |\overrightarrow {CB} | = a\)