Bài 4 trang 27 SGK Hình học 10
Giải bài 4 trang 27 SGK Hình học 10. Chứng minh rằng :
Đề bài
Chứng minh rằng \(|\overrightarrow a + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow {b|} .\)
Phương pháp giải - Xem chi tiết
Dựng các véc tơ \(\overrightarrow a ,\overrightarrow b \) chung gốc.
Sử dụng bất đẳng thức tam giác để chứng minh.
Lời giải chi tiết
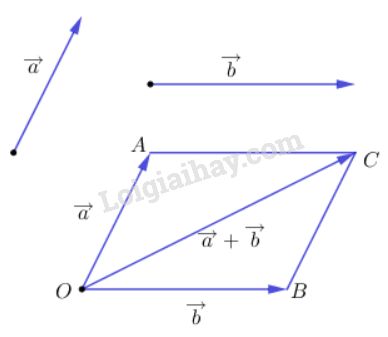
Từ một điểm \(O\) trong mặt phẳng ta dựng vectơ:
\(\eqalign{
& \overrightarrow {OA} = \overrightarrow a \cr
& \overrightarrow {OB} = \overrightarrow b \cr} \)
Và dựng hình bình hành \(OACB\) \( \Rightarrow \overrightarrow {AC} = \overrightarrow {OB} \)
Như vậy:
\(\eqalign{
& OA = |\overrightarrow {OA} | = |\overrightarrow a | \cr
& OB = |\overrightarrow {OB} | = |\overrightarrow b | \cr&\Rightarrow AC = |\overrightarrow {AC} | = |\overrightarrow b | \cr
& \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \Rightarrow \overrightarrow {OC} = \overrightarrow a + \overrightarrow b \cr
& OC = |\overrightarrow {OC} | = |\overrightarrow a + \overrightarrow b | \cr} \)
Áp dụng bất đẳng thức tam giác vào tam giác \(OAC\), ta có:
\(OA + AC ≥ OC \)\( ⇒ |\overrightarrow a + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow {b|} \).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4 trang 27 SGK Hình học 10 timdapan.com"







