Bài 5 trang 27 (Ôn tập chương I - Vectơ) SGK Hình học 10

Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \(O\). Hãy xác định các điểm \(M, N, P\) sao cho:

LG a

\(\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} \)

Lời giải chi tiết:

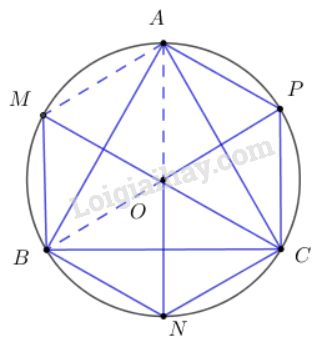
Nối \(OC\) và kéo dài cắt đường tròn tại điểm \(M\)

Dễ thấy, tam giác \(OAM\) là tam giác đều và \(OAMB\) là hình bình hành, cho ta:

  \(\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OM} \)

LG b

\(\overrightarrow {OP}  = \overrightarrow {OC}  + \overrightarrow {OA} \)

Lời giải chi tiết:

Nối \(OB\) và kéo dài cắt đường tròn tại điểm \(P\)

Tương tự như trên ta có:

\(\overrightarrow {OP}  = \overrightarrow {OC}  + \overrightarrow {OA} \)

LG c

\(\overrightarrow {ON}  = \overrightarrow {OB}  + \overrightarrow {OC} \)

Lời giải chi tiết:

 Nối \(OA\) và kéo dài cắt đường tròn tại điểm \(N\)

Tương tự như trên ta có:

\(\overrightarrow {ON}  = \overrightarrow {OB}  + \overrightarrow {OC} \)