Bài 1.61 trang 22 SBT Giải tích 12 Nâng cao

Đề bài

Với giá trị nào của m, phương trình

\(4{x^3} - 3x - 2m + 3 = 0\)

Có một nghiệm duy nhất ?

Lời giải chi tiết

Ta có:

\(\begin{array}{l}4{x^3} - 3x - 2m + 3 = 0\\ \Leftrightarrow 4{x^3} - 3x + 3 = 2m\end{array}\)

Xét hàm \(f\left( x \right) = 4{x^3} - 3x + 3\) trên \(\mathbb{R}\) ta có:

\(\begin{array}{l}y' = 12{x^2} - 3\\y' = 0 \Leftrightarrow 12{x^2} - 3 = 0\\ \Leftrightarrow {x^2} = \frac{1}{4} \Leftrightarrow x =  \pm \frac{1}{2}\end{array}\)

BBT:

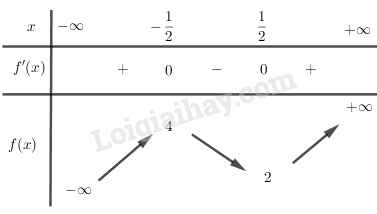
Để phương trình có nghiệm duy nhất thì đường thẳng \(y = 2m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất.

Quan sát BBT ta thấy \(\left[ \begin{array}{l}2m < 2\\2m > 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.\)

Vậy \(m < 1\) hoặc \(m > 2\).