Bài 1.45 trang 19 SBT Giải tích 12 Nâng cao

LG a

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

\(y = {x^3} - 6{x^2} + 9x\)

Lời giải chi tiết:

+) TXĐ: \(D = \mathbb{R}\).

+) Chiều biến thiên:

\(\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty ,\mathop {\lim }\limits_{x \to  - \infty } y =  - \infty \)

\(\begin{array}{l}y' = 3{x^2} - 12x + 9\\y' = 0 \Leftrightarrow 3{x^2} - 12x + 9 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\end{array}\)

BBT:

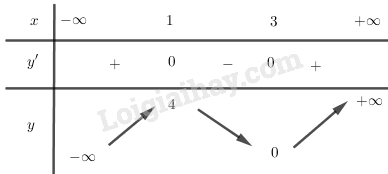
Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).

Hàm số nghịch biến trên \(\left( {1;3} \right)\).

Hàm số đạt cực đại tại \(x = 1,{y_{CD}} = 4\)

Hàm số đạt cực tiểu tại \(x = 3,{y_{CT}} = 0\).

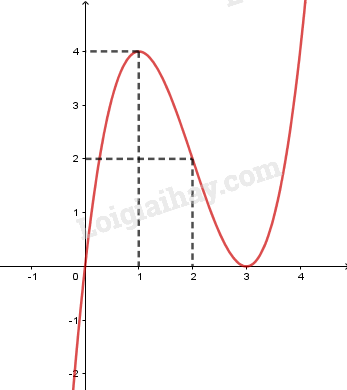
+) Đồ thị:

\(\begin{array}{l}y'' = 6x - 12\\y'' = 0 \Leftrightarrow 6x - 12 = 0\\ \Leftrightarrow x = 2 \Rightarrow y\left( 2 \right) = 2\end{array}\)

Điểm uốn \(I\left( {2;2} \right)\).

Đồ thị hàm số cắt trục tung tại điểm \(\left( {0;0} \right)\).

Điểm cực đại \(\left( {1;4} \right)\) và điểm cực tiểu \(\left( {3;0} \right)\).

Phương trình hoành độ giao điểm:

\(\begin{array}{l}{x^3} - 6{x^2} + 9x = 0\\ \Leftrightarrow x\left( {{x^2} - 6x + 9} \right) = 0\\ \Leftrightarrow x{\left( {x - 3} \right)^2} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right.\end{array}\)

Đồ thị cắt trục hoành tại điểm \(\left( {0;0} \right)\) và tiếp xúc trục hoành tại điểm \(\left( {3;0} \right)\).

LG b

Chứng minh rằng điểm uốn của đường cong (C) là tâm đối xứng của nó

Lời giải chi tiết:

Công thức chuyển hệ tọa độ theo véc tơ \(\overrightarrow {OI} \) là: \(\left\{ \begin{array}{l}x = X + 2\\y = Y + 2\end{array} \right.\)

Phương trình đường cong trong hệ tọa độ IXY là:

\(\begin{array}{l}Y + 2 = {\left( {X + 2} \right)^3} - 6{\left( {X + 2} \right)^2} + 9\left( {X + 2} \right)\\ \Leftrightarrow Y + 2 = {X^3} + 6{X^2} + 12X + 8\\ - 6{X^2} - 24X - 24 + 9X + 18\\ \Leftrightarrow Y + 2 = {X^3} - 3X + 2\\ \Leftrightarrow Y = {X^3} - 3X\end{array}\)

Đây là hàm số lẻ nên đồ thị nhận \(I\) làm tâm đối xứng.

LG c

Với các giá trị nào của m, đường thẳng y = m cắt (C) tại 3 điểm phân biệt ?

Lời giải chi tiết:

Số nghiệm của phương trình bằng số giao điểm của đường thẳng y=m với đồ thị hàm số.

Do đó để phương trình có 3 nghiệm phân biệt thì đường thẳng y=m (song song hoặc trùng Ox và đi qua điểm (0;m)) phải cắt (C) tại 3 điểm phân biệt.

Quan sát đồ thì ta thấy 0 < m < 4 thỏa mãn.