Bài 6 trang 62 SGK Đại số 10

Giải các phương trình.

LG a

\(|3x – 2| = 2x + 3\);

Phương pháp giải:

Bình phương hai vế, chú ý đặt điều kiện cho vế phải không âm rồi mới bình phương.

Lời giải chi tiết:

ĐKXĐ: \(2x + 3 ≥ 0\). Bình phương hai vế thì được:

\({\left( {3x{\rm{ }}-{\rm{ }}2} \right)^2} = {\left( {2x{\rm{ }} + {\rm{ }}3} \right)^2}\)\( \Leftrightarrow {\left( {3x{\rm{ }} - {\rm{ }}2} \right)^2} - {\left( {2x{\rm{ }} + {\rm{ }}3} \right)^2} = {\rm{ }}0\)

\( \Leftrightarrow \left( {3x - 2{\rm{ }} + {\rm{ }}2x + {\rm{ }}3} \right)\left( {3x-2{\rm{ }}-2x-3} \right){\rm{ }} \)\(= {\rm{ }}0\) 

\(\begin{array}{l}
 \Leftrightarrow \left( {5x + 1} \right)\left( {x - 5} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
5x + 1 = 0\\
x - 5 = 0
\end{array} \right.
\end{array}\)

\( \Leftrightarrow \left[ \matrix{
x = - {1 \over 5}\text{ (thỏa mãn )} \hfill \cr 
x = 5\text{ (thỏa mãn )} \hfill \cr} \right.\)

Vậy phương trình đã cho có hai nghiệm.

LG b

\(|2x -1| = |-5x – 2|\);

Phương pháp giải:

Bình phương hai vế.

Lời giải chi tiết:

Bình phương hai vế:

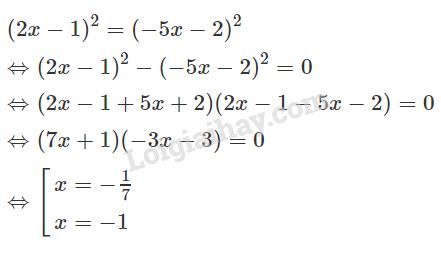
Vậy phương trình có hai nghiệm

LG c

\(\dfrac{x-1}{2x -3}=\dfrac{-3x+1}{|x+1|};\)

Phương pháp giải:

- Xét trường hợp của \(x\) để phá dấu giá trị tuyệt đối.

- Giải phương trình có được và đối chiếu điều kiện đặt ra.

Lời giải chi tiết:

ĐKXĐ: \(x ≠ \dfrac{3}{2}, x ≠ -1\). Quy đồng rồi khử mẫu thức chung

\(\Rightarrow (x – 1)|x + 1| = (2x – 3)(-3x + 1)\)

+)  Với \(x ≥ -1\) ta được:

\(\eqalign{
& (x - 1)(x + 1) = (2x - 3)( - 3x + 1) \cr 
& \Leftrightarrow {x^2} - 1 = - 6{x^2} + 11x - 3 \cr&\Leftrightarrow 7{x^2} - 11x + 2 = 0 \cr 
& \Leftrightarrow \left[ \matrix{
x = {{11 + \sqrt {65} } \over {14}}\text{ (thỏa mãn )}  \hfill \cr 
x = {{11 - \sqrt {65} } \over {14}}\text{ (thỏa mãn )}  \hfill \cr} \right.
& \cr} \)

+) Với \(x < -1\) ta được:

\((x - 1)( - x - 1) = (2x - 3)( - 3x + 1)\)

\(\eqalign{
& \Leftrightarrow - {x^2} + 1 = - 6{x^2} + 11x - 3 \cr&\Leftrightarrow 5{x^2} - 11x + 4 = 0 \cr 
& \Leftrightarrow \left[ \matrix{
x = {{11 + \sqrt {41} } \over {10}}\text{ (loại)}  \hfill \cr 
x = {{11 - \sqrt {41} } \over {10}}\text{ (loại )}  \hfill \cr} \right. \cr} \)

Vậy phương trình đã cho có hai nghiệm.

LG d

\(|2x + 5| = x^2+5x +1\).

Phương pháp giải:

- Xét trường hợp của \(x\) để phá dấu giá trị tuyệt đối.

- Giải phương trình có được và đối chiếu điều kiện đặt ra.

Lời giải chi tiết:

+) Với \(x ≥ \dfrac{-5}{2}\) ta được:

\(\eqalign{
& 2x + 5{\rm{ = }}{x^2} + 5x{\rm{ + }}1 \cr 
& \Leftrightarrow {x^2} + 3x - 4 = 0 \cr 
& \Leftrightarrow \left[ \matrix{
x = 1 \text{ (thỏa mãn )}\hfill \cr 
x = - 4\text{ (loại )} \hfill \cr} \right. \cr} \)

+) Với \(x < \dfrac{-5}{2}\) ta được:

\(\eqalign{
& - 2x - 5{\rm{ = }}{x^2} + 5x{\rm{ + }}1 \cr 
& \Leftrightarrow {x^2} + 7x + 6 = 0 \cr 
& \Leftrightarrow \left[ \matrix{
x = - 6 \text{ (thỏa mãn )}\hfill \cr 
x = - 1\text{ (loại )}  \hfill \cr} \right. \cr} \)

Vậy phương trình đã cho có hai nghiệm \(x=1\) và \(x=-6\).