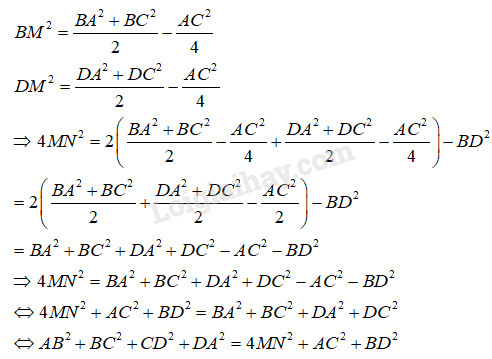Bài 30 trang 66 SGK Hình học 10 nâng cao
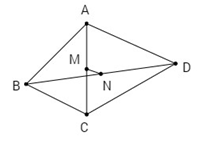
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC và BD.
Đề bài
Cho tứ giác \(ABCD\). Gọi \(M, N\) lần lượt là trung điểm của \(AC\) và \(BD\). Chứng minh rằng:
\(A{B^2} + B{C^2} + C{D^2} + D{A^2}\)\( = A{C^2} + B{D^2} + 4M{N^2}\).
Phương pháp giải - Xem chi tiết
- Áp dụng công thức trung tuyến trong các tam giác:
+ BMD để tính MN.
+ BAC để tính BM.
+ DAC để tính DM.
- Từ đó biến đổi suy ra đpcm.
Lời giải chi tiết
Áp dụng công thức tính trung tuyến, \(MN\) là trung tuyến của tam giác \(BMD\), ta có
\(M{N^2} = {{B{M^2} + D{M^2}} \over 2} - {{B{D^2}} \over 4}\)
\(\Leftrightarrow \,\,4M{N^2} = 2(B{M^2} + D{M^2}) - B{D^2}\)
Mà \(BM, DM\) lần lượt là trung tuyến của tam giác \(ABC, ADC\) nên
Cách khác:
* Áp dụng công thức trung tuyến của tam giác ta có:
\(\begin{array}{l}m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4}\\ \Leftrightarrow \frac{{{b^2} + {c^2}}}{2} = m_a^2 + \frac{{{a^2}}}{4}\\ \Leftrightarrow {b^2} + {c^2} = 2m_a^2 + \frac{{{a^2}}}{2}\,\,\,\left( * \right)\end{array}\)
* Áp dụng công thức (*)
Trong tam giác ABD ta có :
AB2 + AD2 = 2AN2 + BD2/2 (1)
Trong tam giác CBD ta có :
CD2 + CB2 = 2CN2 + BD2/2 (2)
Cộng vế với vế của (1) và (2) ta có :
AB2 + BC2 + CD2 + DA2
= 2(AN2 + CN2) + BD2(3)
Xét tam giác CAN ta có :
AN2 + CN2 = 2MN2 + AC2/2 (4) (vì M là trung điểm AC)
Thay (4) vào (3) ta được :
AB2 + BC2 + CD2 + DA2
= 2[2MN2 + AC2/2] + BD2
= AC2 + BD2 + 4MN2
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 30 trang 66 SGK Hình học 10 nâng cao timdapan.com"