Bài 1, 2, 3 trang 124, 125 SGK Toán 4

Bài 1

Mỗi bài tập dưới đây có nêu kèm theo một câu trả lời đúng. Hãy khoanh vào chữ đặt trước câu trả lời đúng.

a) Trong các số 5451; 5514; 5145; 5541 số chia hết cho 5 là:

A. 5451                     B. 5514                    C. 5145                     D. 5541

Phương pháp giải:

 Số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.

Giải chi tiết:

Trong các số đã cho, số chia hết cho 5 là 5145.

Chọn C.

b) Hùng có 8 viên bi gồm 4 viên bi màu xanh, 3 viên bi màu đỏ, 1 viên bi màu vàng. Phân số chỉ các viên bi màu đỏ trong số viên bi của Hùng là:

A. \( \displaystyle{4 \over 8}\)                   B. \( \displaystyle{3 \over 4}\)                   C. \( \displaystyle{1 \over 8}\)                   D. \( \displaystyle{3 \over 8}\)

Phương pháp giải:

Phân số chỉ các viên bi màu đỏ trong số viên bi của Hùng có tử số là số viên bi màu đỏ, mẫu số là tổng số viên bi của Hùng.

Giải chi tiết:

Phân số chỉ các viên bi màu đỏ trong số viên bi của Hùng là \( \displaystyle{3 \over 8}\).

Chọn D.

c) Phân số \( \displaystyle{5\over 9}\) bằng phân số nào dưới đây:

A. \( \displaystyle{10 \over 27}\)               B. \( \displaystyle{15 \over 18}\)             C. \( \displaystyle{15 \over 27}\)            D. \( \displaystyle{20 \over 27}\)

Phương pháp giải:

Rút gọn các phân số thành phân số tối giản (nếu được). Phân số bằng phân số \( \displaystyle{5\over 9}\) thì rút gọn được thành phân số \( \displaystyle{5\over 9}\).

Giải chi tiết:

Ta có: phân số \( \displaystyle{10 \over 27}\) và \( \displaystyle{20 \over 27}\) là các phân số tổi giản.

Rút gọn hai phân số \( \displaystyle{15 \over 18}\) và \( \displaystyle{15 \over 27}\) ta có:

\(\dfrac{15}{18} = \dfrac{15:3}{18:3} = \dfrac{5}{6}\) ;      \(\dfrac{15}{27} = \dfrac{15:3}{27:3} = \dfrac{5}{9}\).

Vậy phân số \( \displaystyle{5\over 9}\) bằng phân số \( \displaystyle{15 \over 27}\).

Chọn C.

d) Trong các phân số \( \displaystyle{9 \over 8};\,\,\,{9 \over 9};\,\,\,{8 \over 8};\,\,\,{8 \over 9}\) phân số nào bé hơn 1?

A. \( \displaystyle{9 \over 8}\)                  B. \( \displaystyle{9 \over 9}\)                  C. \( \displaystyle{8 \over 8}\)                 D. \( \displaystyle{8 \over 9}\)

Phương pháp giải:

Phân số có tử số bé hơn mẫu số thì phân số đó bé hơn 1.

Giải chi tiết:

 Trong các phân số đã cho, phân só bé hơn 1 là \( \displaystyle{8 \over 9}\).

Chọn D.

Bài 2

Đặt tính rồi tính :

a) 53867 + 49608                                       b) 482 × 307 

c) 864752 – 91846                                     d) 18490 : 215

Phương pháp giải:

Đặt tính rồi tính theo các quy tắc đã học.

Lời giải chi tiết:

Bài 3

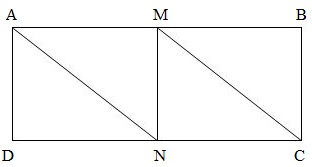
Cho hình chữ nhật ABCD có chiều dài 12cm, chiều rộng 5cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng hình chữ nhật.

a) Giải thích tại sao đoạn thẳng AN và MC song song và bằng nhau.

b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN?

Phương pháp giải:

- Áp dụng tính chất: Hình bình hành có các cặp cạnh đối diện song song và bằng nhau.

- Diện tích hình chữ nhật = chiều dài × chiều rộng.

- Diện tích hình bình hành = độ dài đáy × chiều cao tương ứng.

Lời giải chi tiết:

a) Các đoạn thẳng AN và MC là hai cạnh đối diện của hình bình hành AMCN nên chúng song song và bằng nhau.

b) Diện tích hình chữ nhật ABCD là:

             12 × 5 = 60 (cm²) 

Vì N là trung điểm của cạnh DC nên độ dài đoạn thẳng NC là: 

             12 : 2 = 6 (cm)

Hình bình hành AMCN có chiều cao MN bằng chiều rộng hình chữ nhật nên MN = 5cm.

Diện tích hình bình hành AMCN là :

             6 × 5 = 30 (cm²) 

Ta có: 60 : 30 = 2 (lần)

Vậy diện tích hình chữ nhật ABCD gấp 2 lần diện tích hình bình hành AMCN.