Bài 1, 2, 3, 4, 5 trang 123, 124 SGK Toán 4

Bài 1

Tìm chữ số thích hợp để viết vào chỗ chấm sao cho:

a) 75... chia hết cho 2 nhưng không chia hết cho 5.

b) 75... chia hết cho 2 và chia hết cho 5.

 Số tìm được có chia hết cho 3 không?

c) 75... chia hết cho 9

Số tìm được có chia hết cho 2 và 3 không?

Phương pháp giải:

Áp dụng các dấu hiệu chia hết cho 2; 5; 9; 3:

- Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.

- Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.

- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.

- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.

- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.

Lời giải chi tiết:

a) Có thể viết vào chỗ chấm một trong các chữ số: 2; 4; 6; 8 tức là:

           752, 754, 756, 758

b) Số chia hết cho 2 và chia hết cho 5 thì chữ số tận cùng của số đó phải là 0. Vậy viết 0 vào chỗ chấm:

          750

Ta có: 7 + 5 + 0 = 12;  12 chia hết cho 3.

Vậy số 750 là số chia hết cho 3. 

c) Để số 75... chia hết cho 9 thì 7 + 5 + ... phải chia hết cho 9, hay 12 + ... phải chia hết cho 9.

Vậy ta điền số 6 vào chỗ chấm:     756

Số 756 có chữ số tận cùng là 6 nên chia hết cho 2, số 756 chia hết cho 3 (vì số 756 có tổng các chữ số là 18 và 18 chia hết cho 3).

Vậy số 756 chia hết cho cả 2 và 3.

Bài 2

Mỗi lớp học có \(14\) học sinh trai và \(17\) học sinh gái.

a) Viết phân số chỉ phần học sinh trai trong số học sinh của lớp học đó.

b) Viết phân số chỉ phần học sinh gái trong số học sinh của lớp học đó.

Phương pháp giải:

- Tìm tổng số học sinh của lớp học đó.

- Phân số chỉ phần học sinh trai (hoặc học sinh gái) trong số học sinh của lớp học đó có tử số là số học sinh trai (hoặc học sinh gái) và mẫu số là tổng số học sinh của lớp học.

Lời giải chi tiết:

 Số học sinh của lớp học đó là :

                \(14 + 17 = 31\) (học sinh)

a) Phân số chỉ phần học sinh trai trong số học sinh của lớp học đó là:  \(\dfrac{14}{31}\).

b) Phân số chỉ phần học sinh gái trong số học sinh của lớp học đó là:   \(\dfrac{17}{31}\).

Bài 3

Trong các phân số  \( \dfrac{20}{36}; \;\dfrac{15}{18} ; \;\dfrac{45}{25}; \;\dfrac{35}{63}\) phân số nào bằng \(\dfrac{5}{9}\) ?  

Phương pháp giải:

Rút gọn các phân số đã cho thành phân số tối giản. Các phân số bằng phân số \(\dfrac{5}{9}\) thì rút gọn được thành phân số tối giản là \(\dfrac{5}{9}\).

Lời giải chi tiết:

Rút gọn các phân số đã cho, ta có:

\(\dfrac{20}{36}=\dfrac{20:4}{36:4}=\dfrac{5}{9}\);                                 \(\dfrac{15}{18}=\dfrac{15:3}{18:3}=\dfrac{5}{6}\)

\(\dfrac{45}{25}=\dfrac{45:5}{25:5}=\dfrac{9}{5}\);                                 \(\dfrac{35}{63}=\dfrac{35:7}{63:7}=\dfrac{5}{9}\)

Vậy các phân số bằng \(\dfrac{5}{9}\) là: \(\dfrac{20}{36};\dfrac{35}{63}\).

Bài 4

Viết các phân số: \(\dfrac{8}{12};\dfrac{12}{15};\dfrac{15}{20}\) theo thứ tự từ lớn đến bé.

Phương pháp giải:

- Rút gọn các phân số đã cho thành phân số tối giản.

- So sánh các phân số sau khi rút gọn bằng cách quy đồng mẫu số các phân số đó.

- So sánh các phân số ban đầu rồi sắp xếp theo thứ tự từ lớn đến bé.

Lời giải chi tiết:

Rút gọn các phân số:

\(\dfrac{8}{12}=\dfrac{8:4}{12:4}=\dfrac{2}{3}\);             \(\dfrac{12}{15}=\dfrac{12:3}{15:3}=\dfrac{4}{5}\);             \(\dfrac{15}{20}=\dfrac{15:5}{20:5}=\dfrac{3}{4}\)

Quy đồng mẫu số các phân số: \(\dfrac{2}{3};\dfrac{4}{5};\dfrac{3}{4}\) ta có:

\(\dfrac{2}{3}=\dfrac{2 \times 5 \times 4}{3 \times 5 \times 4}=\dfrac{40}{60}\);          \(\dfrac{4}{5}=\dfrac{4 \times 3 \times 4}{5 \times 3 \times 4}=\dfrac{48}{60}\);         \(\dfrac{3}{4}=\dfrac{3 \times 3 \times 5}{4 \times 3 \times 5}=\dfrac{45}{60}\)

Vì \( \dfrac{48}{60}> \dfrac{45}{60}>\dfrac{40}{60}\) nên \(\dfrac{4}{5} >\dfrac{3}{4}>\dfrac{2}{3}\).

Hay \(\dfrac{12}{15}> \dfrac{15}{20}> \dfrac{8}{12}\).

Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé như sau:   \(\dfrac{12}{15};\;\dfrac{15}{20};\;\dfrac{8}{12}\).

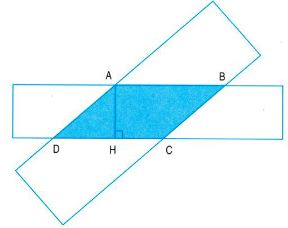
Bài 5

Hai hình chữ nhật có phần chung là hình tứ giác ABCD (xem hình vẽ).

a) Giải thích tại sao hình tứ giác ABCD có từng cặp cạnh đối diện song song.

b) Đo độ  dài các cạnh của hình tứ giác ABCD rồi nhận xét xem từng cặp cạnh đối diện có bằng nhau không?

c) Cho biết hình tứ giác ABCD là hình bình hành có độ dài đáy DC là 4cm, chiều cao AH là 2cm. Tính diện tích của hình bình hành ABCD.

Phương pháp giải:

- Dùng thước kẻ đo độ dài các cạnh của tứ giác ABCD rồi rút ra nhận xét.

- Muốn tính diện tích hình bình hành ta lấy độ dài đáy nhân với chiều cao tương ứng.

Lời giải chi tiết:

 a) Cạnh AB và cạnh AD của tứ giác ABCD thuộc hai cạnh đối diện của hình chữ nhật thứ nhất (hình chữ nhật nằm ngang) nên chúng song song với nhau.

Cạnh DA và cạnh BC thuộc hai cạnh đối diện của hình chữ nhật thứ hai (hình chữ nhật đặt chéo) nên chúng song song nhau.

b) Đo độ dài các cạnh của hình tứ giác ABCD ta có:

AB = 4cm;                                DA = 3cm;  

CD = 4cm;                                BC = 3cm

Do đó AB = CD và DA = BC.

Vậy tứ giác ABCD có từng cặp cạnh đối diện bằng nhau.

c) Diện tích hình bình hành ABCD là:

                   4 × 2 = 8 (cm²)