Giải mục 1 trang 5 , 6, 7 ,8 , 9 SGK Toán 11 tập 1 - Cánh Diều

Hoạt động 1

Nêu định nghĩa góc trong hình học phẳng.

Lời giải chi tiết:

Góc là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc là độ hoặc radian.

Số đo của mỗi góc không vượt quá \({180^ \circ }\)

Luyện tập - Vận dụng 1

Hãy hoàn thành bảng chuyển đổi số đo độ và số đo radian của một số góc sau.

Phương pháp giải:

\(1\,rad = {\left( {\frac{{180}}{\pi }} \right)^0}\); \({1^0} = \left( {\frac{\pi }{{180}}} \right)\,rad\)

Lời giải chi tiết:

Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc sau:

Hoạt động 2

So sánh chiều quay của kim đồng hồ với:

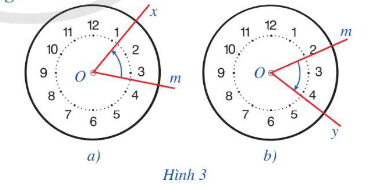
a) Chiều quay từ tia Om đến tia Ox trong Hình 3a.

b) Chiều quay từ tia Om đến tia Oy trong Hình 3b.

Lời giải chi tiết:

a) Chiều quay từ tia Om đến tia Ox trong Hình 3a là chiều quay ngược chiều kim đồng hồ

b) Chiều quay từ tia Om đến tia Oy trong Hình 3b là chiều quay cùng chiều kim đồng hồ.

Luyện tập - Vận dụng 2

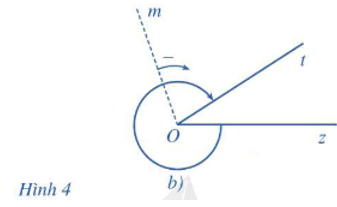
Đọc tên góc lượng giác, tia đầu và tia cuối của góc lượng giác trong Hình 4b.

Lời giải chi tiết:

Trong Hình 4b, góc lượng giác là (Oz,Ot) với tia đầu là tia Oz và tia cuối là tia Ot

Hoạt động 3

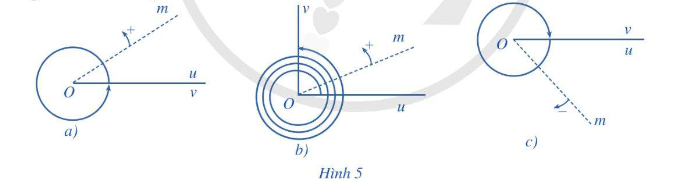
a) Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?

b) Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng ( tức là \(3\frac{1}{4}\)vòng). Hỏi tia đó quét nên một góc bao nhiêu độ?

c) Trong Hình 5x, toa Om quay theo chiều âm đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?

Phương pháp giải:

Một vòng ứng với \({360^ \circ }\)

Lời giải chi tiết:

a) Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng. Tia đó quét nên một góc \({360^ \circ }\)

b) Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng ( tức là \(3\frac{1}{4}\)vòng). Tia đó quét nên một góc \({3.360^ \circ } + \frac{1}{4}{360^ \circ } = {1170^ \circ }\)

c) Trong Hình 5x, toa Om quay theo chiều âm đúng một vòng. Tia đó quét nên một góc -\({360^ \circ }\)

Luyện tập - Vận dụng 3

Hãy biểu diễn trên mặt phẳng góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{5\pi }}{4}\)

Lời giải chi tiết:

Ta có \( - \frac{{5\pi }}{4} =  - \pi  + \left( { - \frac{\pi }{4}} \right)\). Góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{5\pi }}{4}\) được biểu diễn ở hình sau:

Hoạt động 4

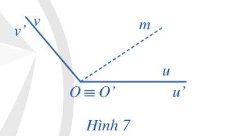
Trong Hình 7, hai góc lượng giác (Ou, Ov), \((O'u',O'v')\)có tia đầu trùng nhau \(Ou \equiv O'u'\), tia cuối trùng nhau \(Ov \equiv O'v'\). Nêu dự đoán về mối liên hệ giữa số đo của hai góc lượng giác trên.

Lời giải chi tiết:

Quan sát Hình 7 ta thấy:

• Tia Om quay (chỉ theo chiều dương) xuất phát từ tia Ou đến trùng với tia Ov rồi quay tiếp một số vòng đến trùng với tia cuối Ov;

• Tia Om quay (chỉ theo chiều dương) xuất phát từ tia \(O'u' \equiv Ou\) đến trùng với tia \(O'v' \equiv Ov\)rồi quay tiếp một số vòng đến trùng với tỉa cuối \(O'v' \equiv Ov\).

Như vậy, sự khác biệt giữa hai góc lượng giác (Ou, Ov) và (O’u’, O’v’) chính là số vòng quay quanh điểm O. Vì vậy, sự khác biệt giữa số đo của hai góc lượng giác đó chính là bội nguyên của \({360^ \circ }\) khi hai góc đó tính theo đơn vị độ (hay bội nguyên của \(2\pi \) rad khi hai góc đó tính theo đơn vị radian).

Luyện tập - Vận dụng 4

Cho góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{4\pi }}{3}\). Cho góc lượng giác  \((O'u',O'v')\) có tia đầu \(O'u' \equiv Ou\), tia cuối \(O'v' \equiv Ov\). Viết công thức biểu thị số  đo góc lượng giác \((O'u',O'v')\)

Phương pháp giải:

Cho hai góc lượng giác (Ou, Ov), \((O'u',O'v')\)có tia đầu trùng nhau \(Ou \equiv O'u'\), tia cuối trùng nhau \(Ov \equiv O'v'\). Khi đó \((Ou,Ov) = (O'u',O'v') + k2\pi ,\,\,\,(k \in \mathbb{Z})\)

Lời giải chi tiết:

Ta có:

\((O'u',O'v') = (Ou,Ov) + k2\pi \,\, = \, - \frac{{4\pi }}{3}\, + k2\pi \,\,\,\,\,\,\,\,(k \in \mathbb{Z})\)

Hoạt động 5

Cho góc ( hình học) xOz, tia Oy nằm trong góc xOz ( Hình 8). Nêu mối liên hệ giữa số đo góc xOz và tổng số đo của hau góc xOy và yOz.

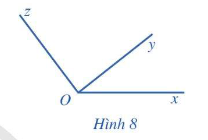
Lời giải chi tiết:

Ta có : \(\widehat {xOz} = \widehat {xOy} + \widehat {yOz}\)

Luyện tập - Vận dụng 5

Cho góc lượng giác (Ou,Ov) có số đo là \( - \frac{{11\pi }}{4}\), góc lượng giác (Ou,Ow) có số đó là \(\frac{{3\pi }}{4}\). Tìm số đo của góc lượng giác (Ov,Ow).

Phương pháp giải:

Áp dụng hệ thức Chasles:

Với ba tia tùy ý Ou,Ov,Ow ta có:

\((Ou,Ov) + (Ov,Ow) = (Ou,Ow) + k2\pi ,\,\,(k \in \mathbb{Z})\).

Lời giải chi tiết:

Theo hệ thức Chasles, ta có:

\(\begin{array}{l}(Ov,Ow) = (Ou,Ov) - (Ou,Ow) + k2\pi \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \, - \frac{{11\pi }}{4} - \frac{{3\pi }}{4} + k2\pi  =  - \frac{7}{2} + k2\pi ,\,\,(k \in \mathbb{Z})\end{array}\)