Bài 63* trang 166 SBT toán 9 tập 1
Giải bài 63* trang 166 sách bài tập toán 9. Cho tam giác ABC vuông tại A. Đường tròn nội tiếp tam giác ABC tiếp xúc với BC tại D. Chứng minh rằng:...
Đề bài
Cho tam giác \(ABC\) vuông tại \(A.\) Đường tròn nội tiếp tam giác \(ABC\) tiếp xúc với \(BC\) tại \(D.\) Chứng minh rằng: \({S_{ABC}} = BD.DC\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm.
+) Sử dụng định lí Py-ta-go: trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
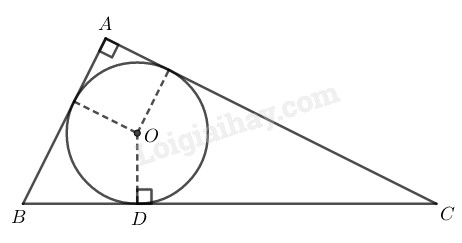
Gọi \(E\) và \(F\) lần lượt là tiếp điểm của đường tròn với \(AB\) và \(AC.\)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
\(AE = AF\)
\( BE = BD\)
\( CD = CF\)
Ta lại có: \(BD = BC - CD\)
\( BE = AB – AE\)
Suy ra: \(BD + BE = AB + BC – (AE + CD )\)
\( = AB + BC – (AE + CE)\)
\(= AB + BC – AC\)
Suy ra: \(BD =\displaystyle {{AB + BC - AC} \over 2}\)
Lại có: \(CD = BC – BD\)
\( CF = AC = AF\)
Suy ra: \(CD + CF \)\(= BC + AC – ( BD + AF)\)
\(= BC + AC – (BE + AE)\)
\(= BC + AC – BA\)
Suy ra: \(CD = \displaystyle {{BC + AC - AB} \over 2}\)
Ta có: \(BD.CD\)\( =\displaystyle {{AB + BC - AC} \over 2}.{{BC + AC - AB} \over 2}\)
\(\displaystyle = {{\left[ {BC - (AC - AB)} \right]\left[ {BC + (AC - AB)} \right]} \over 4}\)
\(\displaystyle ={{B{C^2} - {{(AC - AB)}^2}} \over 4}\)
\( = \displaystyle {{B{C^2} - A{C^2} - A{B^2} + 2AB.AC} \over 4}\) \((1)\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(ABC,\) ta có:
\( BC^2 = AB^2 + AC^2 \;\; (2)\)
Từ \((1)\) và \((2)\) suy ra: \(BD.CD = \displaystyle {{2AB.AC} \over 4} \)\(= {{AB.AC} \over 2}\)
Mà \({S_{ABC}} = \displaystyle {1 \over 2}AB.AC\)
Vậy \({S_{ABC}} = BD.DC.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 63* trang 166 SBT toán 9 tập 1 timdapan.com"







