Bài 49 trang 164 SBT toán 9 tập 1
Giải bài 49 trang 164 sách bài tập toán 9. Cho đường tròn (O), điểm M nằm bên ngoài đường tròn. Kẻ tiếp tuyến MD, ME với đường tròn (D, E là các tiếp điểm). Qua điểm I thuộc cung nhỏ DE, kẻ tiếp tuyến với đường tròn, cắt MD và ME theo thứ tự ở P và Q. Biết MD = 4cm, tính chu vi tam giác MPQ.
Đề bài
Cho đường tròn \((O),\) điểm \(M\) nằm bên ngoài đường tròn. Kẻ tiếp tuyến \(MD, ME\) với đường tròn \((D, E\) là các tiếp điểm)\(.\) Qua điểm \(I\) thuộc cung nhỏ \(DE,\) kẻ tiếp tuyến với đường tròn, cắt \(MD\) và \(ME\) theo thứ tự ở \(P\) và \(Q.\) Biết \(MD = 4cm,\) tính chu vi tam giác \(MPQ.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm.
Lời giải chi tiết
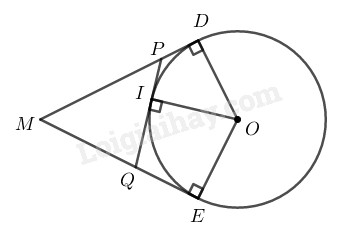
Ta có: \(MD = ME\) (tính chất hai tiếp tuyến cắt nhau)
\( PD = PI\) (tính chất hai tiếp tuyến cắt nhau)
\(QI = QE\) (tính chất hai tiếp tuyến cắt nhau)
Chu vi tam giác \(MPQ\) bằng:
\(MP + PQ + QM\)
\(= MP + PI + IQ + QM\)
\( = MP + PD + QM + QE\)
\(= MD + ME\)
\( = 2.MD\)
\( = 2.4 = 8 (cm)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 49 trang 164 SBT toán 9 tập 1 timdapan.com"







