Bài 6.3 phần bài tập bổ sung trang 167 SBT toán 9 tập 1
Giải bài 6.3 phần bài tập bổ sung trang 167 sách bài tập toán 9. Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ dây CD song song với AB. Chứng minh rằng BC = BD.
Đề bài
Từ điểm \(A\) nằm ngoài đường tròn \((O),\) kẻ các tiếp tuyến \(AB, AC\) với đường tròn. Kẻ dây \(CD\) song song với \(AB.\) Chứng minh rằng \(BC = BD.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Lời giải chi tiết
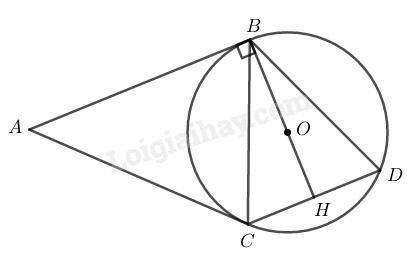
Ta có \(OB ⊥ AB\) (tính chất tiếp tuyến)
\(AB // CD \;\;(gt)\) nên \(OB ⊥ CD.\)
Gọi \(H\) là giao điểm của \(BO\) và \(CD\) thì \(BH ⊥ CD,\) suy ra \(HC = HD\) (tính chất đường kính dây cung)
Do đó \(BC = BD.\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6.3 phần bài tập bổ sung trang 167 SBT toán 9 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6.3 phần bài tập bổ sung trang 167 SBT toán 9 tập 1 timdapan.com"







