Bài 3.78 trang 170 SBT hình học 10

Đề bài

Cho hai điểm \(A\left( {3;0} \right)\), \(B\left( {0;4} \right)\). Đường tròn nội tiếp tam giác \(OAB\) có phương trình là:

A. \({x^2} + {y^2} = 1\) 

B. \({x^2} + {y^2} = 2\) 

C. \({x^2} + {y^2} - 2x - 2y + 1 = 0\) 

D. \({x^2} + {y^2} - 6x - 8y + 25 = 0\) 

Lời giải chi tiết

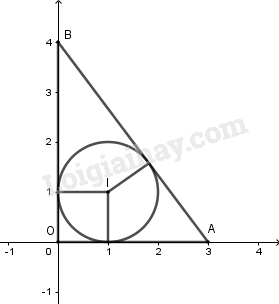
Gọi \(I\left( {a;b} \right)\) là tâm đường tròn nội tiếp tam giác \(OAB\) \(\left( {0 < a,b < 3} \right)\) 

Đường thẳng \(AB\) đi qua \(A\left( {3;0} \right),B\left( {0;4} \right)\) nên có phương trình \(\dfrac{x}{3} + \dfrac{y}{4} = 1 \Leftrightarrow 4x + 3y - 12 = 0\) 

\(d\left( {I,OA} \right) = d\left( {I,OB} \right) = d\left( {I,AB} \right)\) \( \Leftrightarrow \left| b \right| = \left| a \right| = \dfrac{{\left| {4a + 3b - 12} \right|}}{{\sqrt {{4^2} + {3^2}} }}\) 

Dễ thấy \(a,b > 0\) nên \(a = b\).

Do đó \(a = \dfrac{{\left| {4a + 3a - 12} \right|}}{5}\) \( \Leftrightarrow 5a = \left| {7a - 12} \right|\) \( \Leftrightarrow 25{a^2} = 49{a^2} - 168a + 144\) \( \Leftrightarrow 24{a^2} - 168a + 144 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}a = 6\left( L \right)\\a = 1\left( {TM} \right)\end{array} \right.\) 

Do đó \(I\left( {1;1} \right),R = 1\) nên ta có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\) hay \({x^2} + {y^2} - 2x - 2y + 1 = 0\).

Chọn C.