Bài 36 trang 108 SBT toán 9 tập 1

Trong mặt phẳng tọa độ, các đỉnh của tam giác \(ABC\) có tọa độ như sau: \(A(1 ; 1) ; B(5 ; 1) ; C(7 ; 9).\) 

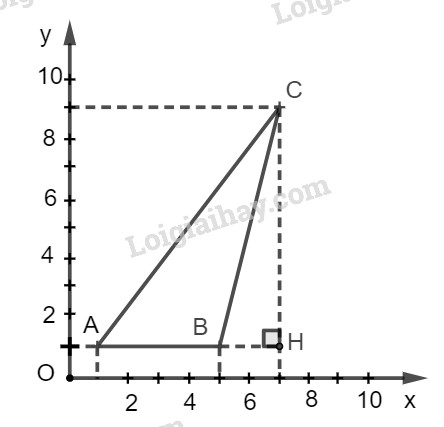
Hãy tính:

LG a

Giá trị của \(tg\widehat {BAC}\) (làm tròn đến chữ số thập phân thứ tư);

Phương pháp giải:

Các tỉ số lượng giác của góc nhọn  (hình) được định nghĩa như sau:

 \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}};\)\(\tan \alpha  = \dfrac{{AB}}{{AC}};\cot \alpha  = \dfrac{{AC}}{{AB}}.\) 

Định lý Pytago vào tam giác ABC vuông tại A.  

\(A{B^2} + A{C^2} = B{C^2}\)

Lời giải chi tiết:

Vì tam giác \(ACH\) vuông tại \(H\) nên ta có:

\(tg\widehat {HAC} = \dfrac{{CH}}{{AH}}\)\( = \dfrac{{9 - 1}}{{7 - 1}} = \dfrac{8}{6} \approx 1,3333\) 

Mà \(A, B, H\) thẳng hàng nên suy ra:

\(tg\widehat {BAC} = tg\widehat {HAC} \approx 1,3333\) 

LG b

Độ dài của cạnh \(AC\).  

Phương pháp giải:

Các tỉ số lượng giác của góc nhọn  (hình) được định nghĩa như sau:

 \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}};\)\(\tan \alpha  = \dfrac{{AB}}{{AC}};\cot \alpha  = \dfrac{{AC}}{{AB}}.\) 

Định lý Pytago vào tam giác ABC vuông tại A.  

\(A{B^2} + A{C^2} = B{C^2}\)

Lời giải chi tiết:

Áp dụng định lí Pytago vào tam giác vuông \(ACH\), ta có: 

\(A{C^2} = C{H^2} + A{H^2}\) 

Suy ra: \(AC = \sqrt {C{H^2} + A{H^2}}\)\(  = \sqrt {{8^2} + {6^2}}  = \sqrt {100}  = 10\)