Bài 2.14 phần bài tập bổ sung trang 110 SBT toán 9 tập 1
Giải bài 2.14 phần bài tập bổ sung trang 110 sách bài tập toán 9. Giải bài Cho tam giác ABC vuông tại A
Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), có \(AB = \dfrac{1}{3}BC\). Hãy tính \(sinC, cosC, tgC, cotgC.\)
Phương pháp giải - Xem chi tiết
- Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
- Ta sử dụng các kiến thức sau:
\({\sin ^2}\alpha + {\cos ^2}\beta = 1\)
\(tg\alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};{\mathop{\rm cotg}\nolimits} \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}\)
\(tg\alpha .\cot g\alpha = 1.\)
Lời giải chi tiết
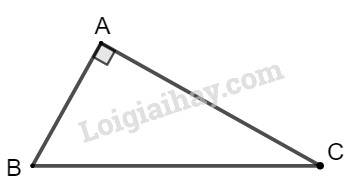
Do \(AB = \dfrac{1}{3}BC\) nên \(\sin C = \dfrac{{AB}}{{BC}} = \dfrac{1}{3}.\) Từ đó
\(\eqalign{
& \cos C = \sqrt {1 - \dfrac{1}{9}} = \dfrac{{2\sqrt 2 }}{ 3}, \cr
& tgC = \dfrac{{\sin C}}{{\cos C}} = \dfrac{1}{ {2\sqrt 2 }} = \dfrac{{\sqrt 2 }}{4}, \cr
& \cot gC = \dfrac{4}{ {\sqrt 2 }} = 2\sqrt {2}. \cr} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.14 phần bài tập bổ sung trang 110 SBT toán 9 tập 1 timdapan.com"







