Bài 25 trang 107 SBT toán 9 tập 1
Giải bài 25 trang 107 sách bài tập toán 9. Tìm giá trị x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình 10, biết rằng:..
Đề bài
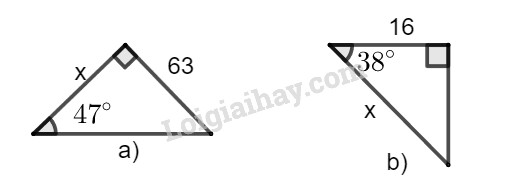
Tìm giá trị \(x\) (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình 10, biết rằng:
\(tg47^\circ \approx 1,072;\cos 38^\circ \approx 0,788.\)
Phương pháp giải - Xem chi tiết
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Định lí Pytago vào tam giác ABC vuông tại A: \(A{B^2} + A{C^2} = B{C^2}.\)
Lời giải chi tiết
a) Hình a
Ta có: \(\tan47^\circ = \dfrac{{63}}{x}.\) Suy ra: \(x = \dfrac{{63}}{ {\tan47^\circ }} \approx \dfrac{{63}}{{1,072}} = 58,769\)
b) Hình b
Ta có: \(\cos 38^\circ = \dfrac{{16}}{x}.\) Suy ra: \(x = \dfrac{{16}}{{\cos 38^\circ }} \approx \dfrac{{16} }{{0,788}} = 20,305\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 25 trang 107 SBT toán 9 tập 1 timdapan.com"







