Bài 2.5, 2.6, 2.7, 2.8 phần bài tập bổ sung trang 109 SBT toán 9 tập 1

Bài 2.5

Xét hình bs. 4. Tìm đẳng thức đúng trong các bài từ 2.5 đến 2.8.

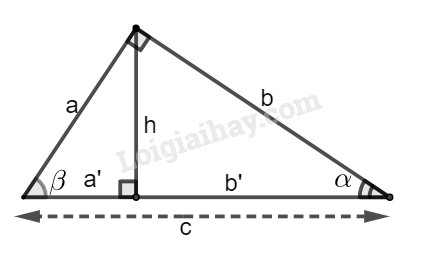
(A) \(\sin \alpha  = \sin \beta \);

(B) \(\sin \alpha  = \cos \beta\);

(C) \(\sin \alpha  = tg\beta \);

(D) \(\sin \alpha  = {\mathop{\rm cotg}\nolimits} \beta \).

Phương pháp giải:

Các tỉ số lượng giác của góc nhọn  (hình) được định nghĩa như sau: 

 \(\sin \alpha  = \dfrac{{AB}}{{BC}};\cos \alpha  = \dfrac{{AC}}{{BC}};\)\(\tan \alpha  = \dfrac{{AB}}{{AC}};\cot \alpha  = \dfrac{{AC}}{{AB}}.\) 

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Với hai góc \(\alpha ,\beta \) sao cho  \(\alpha  + \beta  = 90^\circ \)

Ta có: \(\sin \alpha  = \cos \beta ;\) \(\sin \beta  = \cos \alpha ;\)\(\tan \alpha  = \cot \beta ;\) \(\tan \beta  = \cot \alpha. \)

Lời giải chi tiết:

Đặt tên hình như hình dưới đây:

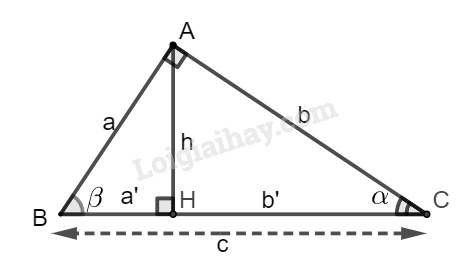
Xét tam giác ABC ta có:

\(\alpha  + \beta  = 90^\circ \)

Vậy \(\alpha, \beta\) là hai góc phụ nhau:

\(\sin \alpha  = c{\rm{os}}\beta. \)

Vậy đáp án đúng là (B).   

Bài 2.6

(A) \(\cos \alpha  = \cos \beta \);

(B) \(\cos \alpha  = tg\beta \);

(C) \(\cos \alpha  = {\mathop{\rm cotg}\nolimits} \beta \); 

(D) \(\cos \alpha  = \sin \beta \)

Lời giải chi tiết:

Xét tam giác ABC ta có:

\(\alpha  + \beta  = 90^\circ \)

Vậy \(\alpha, \beta\) là hai góc phụ nhau:

\(\cos \alpha  = s{\rm{in}}\beta. \)

Vậy đáp án đúng là (D).

Bài 2.7

(A) \(tg\alpha  = tg\beta \);

(B) \(tg\alpha  = cotg\beta \);

(C) \(tg\alpha  = \sin \beta \);

(D) \(tg\alpha  = \cos \beta \).

Lời giải chi tiết:

Xét tam giác ABC ta có:

\(\alpha  + \beta  = 90^\circ \)

Vậy \(\alpha, \beta\) là hai góc phụ nhau:

\(\ tg \alpha  = c{\rm{otg}}\beta. \)

Vậy đáp án đúng là (B).

Bài 2.8

(A) \(\cot g\alpha  = tg\beta \);

(B) \(\cot g\alpha  = cotg\beta \);

(C) \(\cot g\alpha  = \cos \beta \); 

(D) \(\cot g\alpha  = \sin \beta \).

Lời giải chi tiết:

Xét tam giác ABC ta có:

\(\alpha  + \beta  = 90^\circ \)

Vậy \(\alpha, \beta\) là hai góc phụ nhau:

\(\ cotg \alpha  = t{\rm{g}}\beta. \)

Vậy đáp án đúng là (A).