Câu 3.47 trang 148 sách bài tập Giải tích 12 Nâng cao

Tính diện tích hình phẳng giới hạn bởi:

LG a

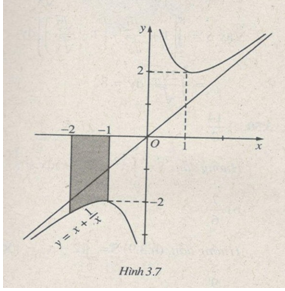
Đồ thị hàm số \(y = x + {1 \over x}\), trục hoành,  đường thẳng \(x =  - 2\) và đường thẳng \(x =  - 1\)

Lời giải chi tiết:

\(S = \int\limits_{ - 2}^{ - 1} {\left| {1 + {1 \over x}} \right|} dx\)  (h.3.7)

$$ =  - \int\limits_{ - 2}^{ - 1} {\left( {1 + {1 \over x}} \right)} \,dx = \left( { - x - \ln |x|} \right)|_{ - 2}^{ - 1} = 1 + \ln 2$$

LG b

Đồ thị hàm số \(y = 1 - {1 \over {{x^2}}}\), trục hoành, đường thẳng \(x = 1\) và đường thẳng \(x = 2\)

Lời giải chi tiết:

\(S = \int\limits_1^2 {\left( {1 - {1 \over {{x^2}}}} \right)dx} = \left( {x + {1 \over x}} \right)|_1^2 = 0,5\)

LG c

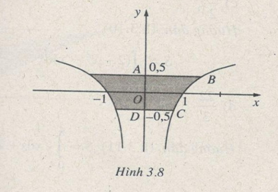
Đồ thị hàm số \(y = 1 - {1 \over {{x^2}}}\), đường thẳng  \(y =  - {1 \over 2}\) và đường thẳng \(y = {1 \over 2}\)

Lời giải chi tiết:

Diện tích hình thang cong ABCD là \(\int\limits_{ - {1 \over 2}}^{{1 \over 2}} {{{dy} \over {\sqrt {1 - y} }}}  = \sqrt 6  - \sqrt 2 \)   (h.3.8)

Do đó diện tích hình phẳng cần tìm là: \(2\left( {\sqrt 6  - \sqrt 2 } \right)\)