Bài 7 trang 78 SGK Đại số 10 nâng cao
Dựa vào hình bên, tìm các giá trị của a để phương trình: 3x + 2 x = -x2 + x + a có nghiệm dương.
Đề bài
Dựa vào hình bên, tìm các giá trị của a để phương trình: \(3x + 2 = - {x^2} + x + a\) có nghiệm dương.
Khi đó, hãy tìm nghiệm dương của phương trình.
Phương pháp giải - Xem chi tiết
Biến đổi phương trình đã cho sao cho biểu thức của mỗi vế xuất hiện trong hình trên
Lời giải chi tiết
Phương trình đã cho tương đương:
\(3x{\rm{ }} + {\rm{ }}2= {\rm{ }} - {x^2} + {\rm{ }}x{\rm{ }} + {\rm{ }}a{\rm{ }}\)
\( \Leftrightarrow 3x + 2 + {x^2} - x = a\)
\(\Leftrightarrow {\rm{ }}{x^2} + {\rm{ }}2x{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}a\) (*)
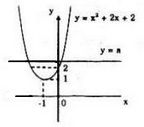
Số nghiệm của phương trình (*) là số giao điểm của (P): \(x^2+ 2x + 2\) và đường thẳng d: \(y = a\)
và mỗi nghiệm tương ứng với 1 hoành độ giao điểm của hai đồ thị.
Dựa vào đồ thị ta thấy:
Phương trình có nghiệm dương khi và chỉ khi đường thẳng y=a cắt (P) tại điểm có hoành độ > 0 ứng với \(a > 2\)
Vậy a > 2.
Lại có:
\(\begin{array}{l}
3x + 2 = - {x^2} + x + a\\
\Leftrightarrow {x^2} + 2x + 2 - a = 0\\
\Delta ' = {1^2} - 1.\left( {2 - a} \right) = a - 1\\
\Rightarrow {x_{1,2}} = - 1 \pm \sqrt {a - 1}
\end{array}\)
Khi đó nghiệm dương của phương trình là \(x = - 1 + \sqrt {a - 1} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7 trang 78 SGK Đại số 10 nâng cao timdapan.com"







